Motivated by the study of noncommutative isolated singularities, the He-Van Oystaeyen-Zhang introduced in [1] the concept of Hopf dense Galois extensions over a field. Hopf dense Galois extensions provide candidates of noncommutative resolutions of quotient isolated singularities. However, it is usually difficult to see when a Hopf action or coaction on an algebra results a Hopf dense Galois extension. When the algebra $ A $ under consideration has a big center, namely, $ A $ is finitely generated over its center, then the problem becomes relatively easy [2]. Indeed, we may use the mod-$ p $ method to reduce the problem to algebras over fields with positive characteristic. For example, if $ A $ is a universal enveloping algebra of a finite dimensional Lie algebra, or $ A $ is a Weyl algebra over a field of characteristic $ p>0 $, then $ A $ is finitely generated over its center. One of the essential parts to use the mod-$ p $ method is to find orders of Hopf actions. Hence it is necessary to consider the Hopf (co) actions and Hopf dense Galois extensions over a commutative domain.

In this paper, we introduce the concept of Hopf dense Galois extensions over a commutative domain. The theory involves several torsion theories. We show that Hopf dense Galois extensions work well. In particular, we prove that a weaker version of Auslander theorem holds for Hopf dense Galois extensions over a commutative domain (cf. Theorem 3.7).

Hopf dense Galois extensions depend on the Hopf algebra (co) actions on the algebra under consideration. It was shown in [3, 4] that not too many semisimple Hopf algebras act inner faithfully on a graded commutative domain or Weyl algebras. Let $ R $ be a commutative domain of characteristic zero and let $ \mathbb{k} $ be an algebraically closed field containing $ R $ as its subring. Assume that $ H $ is a Hopf $ R $-algebra which is a finitely generated free $ R $-module. Suppose that $ H $ coacts on an almost commutative algebra $ A $ and the coaction preserves the filtration. If $ A $ is Hopf dense Galois over the invariant subalgebra $ A^{\hbox{co}H} $, then $ H^*\otimes_R\mathbb{k} $ is isomorphic to a group algebra over $ \mathbb{k} $ (cf. Theorem 4.10). Theorem 4.10 applies to Hopf algebra coactions on Sridharan enveloping algebras which including universal enveloping algebras of finite dimensional Lie algebras and Weyl algebras. In particular, if $ H $ is a finite dimensional Hopf algebra over an algebraically closed field of characteristic zero which acts on a Sridharan enveloping algebra $ U_f(\mathfrak{g}) $ such that the action preserves the filtration of $ U_f(\mathfrak{g}) $ and the associated graded algebra of $ U_f(\mathfrak{g}) $ is a Hopf dense Galois extension on its invariant subalgebra, then $ H $ is isomorphic to a group algebra (cf. Corollary5.12). This result partially generalizes [3, Theorem 4.2].

Let $ R $ be a commutative domain. Let $ Q $ be the quotient field of $ R $. Given a noetherian $ R $-algebra $ A $, the localizing $ A\otimes_R Q $ is a $ Q $-algebra. For simplicity, we write $ A_Q $ for the $ Q $-algebra $ A\otimes_R Q $. Similarly, if $ M $ is a right $ A $-module, then $ M_Q: = M\otimes_R Q $ is a right $ A_Q $-module. We will say that $ M $ is $ R $-torsion free if for any $ x \in M, r \in R $, $ xr = 0 $ implies $ r = 0 $. The localizing functor $ -\otimes_RQ $ induces an exact functor $ (-)_Q:\;\text{Mod}\; A\longrightarrow\;\text{Mod}\; A_Q $. We will frequently use the following properties of localizations.

Lemma 2.1 (ⅰ) Let $ M $ and $ N $ be $ R $-modules. Then $ (M\otimes_RN)_Q\cong M_Q\otimes_QN_Q $.

(ⅱ) Let $ M $ be a right $ A $-module and $ N $ be a left $ A $-module. Then $ (M\otimes_AN)_Q\cong M_Q\otimes_{A_Q}N_Q $.

Let us recall some settings in [1]. For a right $ A_Q $-module $ M $, an element $ x\in M $ is called an $ A_Q $-torsion element if $ xA_Q $ is a finite dimensional $ Q $-vector space. Let $ \Gamma_{A_Q}(M) $ be the subset of $ M $ consisting of all the $ A_Q $-torsion elements. Then $ \Gamma_{A_Q}(M) $ is a right $ A_Q $-submodule of $ M $. If $ M = \Gamma_{A_Q}(M) $, then $ M $ is called an $ A_Q $-torsion module. Let $ \operatorname {Tor} A_Q $ be the full subcategory of $ \;\text{Mod}\; A_Q $ consisting of $ A_Q $-torsion modules. Then $ \operatorname {Tor} A_Q $ is a Serre subcategory of $ \;\text{Mod}\; A_Q $. Denote the quotient category

$ Q\;\text{Mod}\; A_Q: = \frac{\;\text{Mod}\; A_Q}{\operatorname {Tor} A_Q}. $

We refer to the book [5] for the properties of the torsion theory and quotient categories.

Consider the composition of exact functors

$ F: \;\text{Mod}\; A \overset{{{\left( - \right)}_{Q}}}{\mathop{\to }}\, \;\text{Mod}\; A_Q \overset{{\pi} }{\mathop{\to }}Q\;\text{Mod}\; A_Q. $

Let $ \operatorname {Tor} A $ be the full subcategory of $ \;\text{Mod}\; A $ consisting of right $ A $-modules $ M $ such that $ F(M) = 0 $. We will say that $ M $ is torsion if $ M \in \operatorname {Tor} A $. Let $ \varphi:M\to M_Q $ be the localizing map. We have the following easy observation.

Lemma 2.2 A right $ A $-module $ M $ is in $ \operatorname {Tor} A $ if and only if for each $ x\in M $, $ \varphi(x)A_Q $ is finite dimensional over $ Q $.

For a right $ A $-module $ M $, let $ \Gamma_A(M) = \{x\in M | \varphi(x)A_Q\text{ is finite dimensional}\}. $ Then $ \Gamma_A(M) $ is a torsion submodule of $ M $.

Lemma 2.3 With the above notions, we have

(ⅰ) $ \Gamma_A(M) $ is the largest torsion submodule of $ M $ and $ M/\Gamma_A(M) $ is torsion free, which is to say, $ \Gamma_A(M/\Gamma_A(M)) = 0 $.

(ⅱ) $ \Gamma_A(M)_Q = \Gamma_{A_Q}(M_Q) $.

Proof Statement (ⅰ) is easy to check. We next prove statement (ⅱ). For $ x \in M $ and an nonzero element $ s \in R $, we have $ (x/s) A_Q = \varphi(x)A_Q $. It follows that $ (x/s)A_Q $ is finite dimensional if and only if $ \varphi(x)A_Q $ is finite dimensional. Hence $ \Gamma_A(M)_Q = \Gamma_{A_Q}(M_Q) $.

The subcategory $ \operatorname {Tor} A $ is a Serre subcategory of $ \;\text{Mod}\; A $. Denote the quotient category

$ Q\;\text{Mod}\; A : = \frac{\;\text{Mod}\; A}{\operatorname {Tor} A}. $

Then we obtain an exact functor (use the same notation)

$ \begin{equation} (-)_{Q}:Q\;\text{Mod}\; A\longrightarrow Q\;\text{Mod}\; A_Q. \end{equation} $

(2.1)

As usual conventions, for an object $ M\in \;\text{Mod}\; A $, the corresponding object in $ Q\;\text{Mod}\; A $ is denoted by $ \mathcal{M} $, and the object in $ Q\;\text{Mod}\; A_Q $ corresponding to $ M_Q $ is denoted by $ \mathcal{M}_Q $.

Let $ M $ and $ N $ be right $ A $-modules. Assume that $ M $ is finitely generated. It is well known

$ \begin{equation} \operatorname {Hom}_A(M, N)_Q\cong \operatorname {Hom}_{A_Q}(M_Q, N_Q). \end{equation} $

(2.2)

We next show that the above isomorphism may be extended to the quotient categories.

Lemma 2.4 Let $ M $ be a right $ A $-module. Let $ L $ be an $ A_Q $-submodule of $ M_Q $ such that $ M_Q/L $ is finite dimensional. Then there is an $ A $-submodule $ K $ of $ M $ such that $ M_Q/L\cong M_Q/K_Q $ and $ M/K $ is $ R $-torsion free.

Proof Let $ \varphi:M\to M_Q $ be the localizing map, and $ K = \{m\in M|\varphi(m)\in L\} $. Then $ L = K_Q $. By the construction, we see that $ M/K $ is $ R $-torsion free.

Proposition 2.1 Let $ M $ be a finitely generated right $ A $-module. For every $ N\in\;\text{Mod}\; A $, we have

$ \operatorname {Hom}_{Q\;\text{Mod}\; A_Q}(\mathcal{M}_Q, \mathcal{N}_Q)\cong\operatorname {Hom}_{Q\;\text{Mod}\; A}(\mathcal{M}, \mathcal{N})_Q. $

Proof We have the following computations

$ \begin{array}{cll} \operatorname {Hom}_{Q\;\text{Mod}\; A_Q}(\mathcal{M}_Q, \mathcal{N}_Q)& = &\underrightarrow\lim\operatorname {Hom}_{A_Q}(L, N_Q/\Gamma_{A_Q}(N_Q))\\ & = &\underrightarrow\lim\operatorname {Hom}_{A_Q}(K_Q, N_Q/\Gamma_{A_Q}(N_Q)), \end{array} $

where the first limit runs over all the $ A_Q $-submodules $ L $ of $ M_Q $ such that $ M_Q/L $ is finite dimensional, and the second limit runs over all the $ A $-submodules $ K $ such that $ M_Q/K_Q\cong (M/K)_Q $ is finite dimensional. Let $ T = \Gamma_{A}(N) $. Then $ T_Q = \Gamma_{A_Q}(N_Q) $ by Lemma 2.3. Hence we have

$ \begin{array}{cll} &&\underrightarrow\lim\operatorname {Hom}_{A_Q}(K_Q, N_Q/\Gamma_{A_Q}(N_Q))\\&\cong&\underrightarrow\lim\operatorname {Hom}_{A_Q}(K_Q, N_Q/T_Q) \cong\underrightarrow\lim\operatorname {Hom}_{A_Q}(K_Q, (N/T)_Q)\\ &\cong&\underrightarrow\lim\operatorname {Hom}_{A}(K, N/T)_Q = \operatorname {Hom}_{\text{QMod} A}(\mathcal{M}, \mathcal{N})_Q. \end{array} $

In this section, $ R $ is a noetherian commutative domain. Let $ Q $ be its quotient field. An $ R $-module $ M $ is said to be quotient-finite if $ M_Q $ is finite dimensional.

Suppose that $ A $ is a noetherian $ R $-algebra which is projective as an $ R $-module. Let $ H $ be a Hopf $ R $-algebra which is a finitely generated free $ R $-module. Assume that $ H $ coacts on $ A $ so that $ A $ is a right $ H $-comodule algebra through the coaction $ \rho:A\to A\otimes_R H $. As the usual convention, we denote $ A^{\text {co}H} = \{a\in A|\rho(a) = a \otimes 1\} $ the coinvariant subalgebra of $ A $.

We next extend the concept of Hopf dense Galois extension (cf. [1]) to algebras over a ring. Consider the following map

$ \beta:A\otimes_{A^{\text {co}H}}A\to A\otimes_R H, \ a\otimes b\mapsto (a\otimes1)\rho(b). $

We call $ A/A^{\text {co}H} $ is a Hopf dense Galois extension if the cokernel of $ \beta $ is quotient-finite. Note that if $ \beta $ is an epimorphism, then $ A/A^{\text {co}H} $ is a classical Hopf Galois extension (cf. [6, 7]).

Applying the localizing functor $ (-)_Q $ to the algebra $ A $ and the Hopf algebra $ H $, we obtain a finite dimensional Hopf algebra $ H_Q $ and a right $ H_Q $-comodule algebra $ A_Q $. Note that the coaction of $ H_Q $ on $ A_Q $ is the map $ \rho_Q:A_Q\to A_Q\otimes_Q H_Q $.

Lemma 3.5 With the notions as above, $ (A^{\text {co}H})_Q\cong (A_Q)^{\text {co}H_Q} $.

Proof Let $ \varphi:A\to A_Q $ and $ \phi:H\to H_Q $ be the localizing maps. Applying $ (-)_Q $ to the inclusion map $ A^{\text {co}H}\to A $, we obtain that $ (A^{\text {co}H})_Q $ is contained in $ (A_Q)^{\text {co}H_Q} $. On the other hand, assume $ a\in A $ and $ \rho_Q(\varphi(a)) = \varphi(a)\otimes_Q 1 $. Since $ H $ is a finitely generated free $ R $-module and $ R $ is a noetherian commutative domain, we extend the unit $ 1 $ of $ R $ to an $ R $-basis $ h_0 = 1, h_1, \dots, h_n $ of $ H $. Then we may write $ \rho(a) = \sum\limits_{i = 0}^na_i\otimes_R h_i $. Then $ \rho_Q(\varphi(a)) = \sum\limits_{i = 0}^n\varphi(a_i)\otimes_Q \phi(h_i) $. Since $ H $ is free, $ \phi(h_0), \dots, \phi(h_n) $ is a $ Q $-basis of $ H_Q $. Comparing with the assumption $ \rho_Q(\varphi(a)) = \varphi(a)\otimes_Q1 $, we obtain $ \varphi(a_0) = \varphi(a) $ and $ \varphi(a_i) = 0 $ for $ i = 1, \dots, n $. Since $ A $ is projective as an $ R $-module, it is $ R $-torsion free, hence $ \varphi $ is injective. It follows that $ a_0 = a $ and $ a_i = 0 $ for $ i = 1, \dots, n $. Hence $ \rho(a) = a\otimes_R1 $.

Proposition 3.2 Let $ A $ be an $ R $-algebra which is projective as an $ R $-module, and let $ H $ be an $ R $-Hopf algebra which is $ R $-free. Assume $ A $ is a right $ H $-comodule algebra. Then $ A/A^{\text {co}H} $ is Hopf dense Galois if and only if $ A_Q/(A_Q)^{\text {co}H_Q} $ is Hopf dense Galois.

Proof Applying $ (-)_Q $ to the map $ \beta:A\otimes_{A^{\text {co}H}}A\to A\otimes_R H $, we obtain

$ \beta_Q:A_Q\otimes_{(A_Q)^{\text {co}H_Q}} A_Q \to A_Q\otimes_Q H_Q $

by Lemma 3.5. Then the condition that the cokernel of $ \beta_Q $ is finite dimensional implies both $ A/A^{\text {co}H} $ and $ A_Q/(A_Q)^{\text {co}H_Q} $ are Hopf dense Galois.

Since the torsion functor $ \Gamma_A $ is left exact, it has right derived functors. Let $ R^i\Gamma_A $ $ (i\ge0) $ denotes the $ i $-th right derived functor of $ \Gamma_A $. Similarly, we have $ R^i\Gamma_{A_Q} $.

Lemma 3.6 If $ R^i\Gamma_A(M) = 0 $ for all $ i\leq k $, then $ R^i\Gamma_{A_Q}(M_Q) = 0 $ for all $ i\leq k $.

Proof Let $ 0\to M\to I^0\to I^1\to\cdots\to I^k\to\cdots $ be an injective resolution of $ M $. Since the localizing functor $ (-)_Q $ preserves injective modules, it follows that $ 0\to M_Q\to I_Q^0\to I_Q^1\to\cdots\to I_Q^k\to\cdots $ is an injective resolution of $ M_Q $. Let $ I^\bullet $ be the complex $ 0\to I^0\to\cdots\to I^k\to \cdots $. By Lemma 2.3, $ R^i\Gamma_{A_Q}(M_Q) = H^i\Gamma_{A_Q}(I^\bullet_Q)\cong H^i(\Gamma_A(I^\bullet)_Q)\cong H^i(\Gamma_A(I^\bullet))_Q = R^i\Gamma_A(M)_Q $. So $ R^i\Gamma_{A_Q}(M_Q) = 0 $ for all $ i\leq k $ in case $ R^i\Gamma_A(M) = 0 $ for $ i\leq k $.

Since by assumption $ H $ is a finitely generated $ R $-algebra, then similar to equation (2.2), we have an isomorphism of Hopf algebras $ \operatorname {Hom}_R (H, R) \otimes_R Q \cong \operatorname {Hom}_Q (H \otimes_R Q, Q). $ Thus we can write

$ \begin{equation} H^*_Q = (H^*)_Q \cong (H_Q)^*, \end{equation} $

(3.1)

where $ H^* = \operatorname {Hom}_R (H, R) $ is the dual Hopf algebra of $ H $.

An important feature of Hopf dense Galois extensions over a field is the truth of Auslander theorem (cf. [1, Theorem 3.10]). Note that Theorem 3.10 of [1] is still true if the characteristic is positive. Next result shows that a weaker version of Auslander theorem holds for Hopf dense Galois extensions over a commutative domain.

Theorem 3.7 Let $ A $ and $ H $ be the algebras as in the beginning of this section. Assume further that $ H_Q $ is cosemisimple. If $ A/A^{\text {co}H} $ is a Hopf dense Galois extension, and $ R^i\Gamma_A(A) = 0 $ for $ i\leq2 $, then the natural map

$ \psi:A\#H^*\longrightarrow \operatorname {End}_{A^{\text {co}H}}(A), a\otimes\alpha\mapsto [b\mapsto a(\alpha\cdot b)] $

is injective. Moreover, for each $ f\in \operatorname {End}_{A^{\text {co}H}}(A) $, there exist $ 0\neq r\in R $ and $ \sum\limits_{i = 1}^na_i\# \alpha_i\in A\#H^* $ such that $ rf(b) = \sum\limits_{i = 1}^na_i(\alpha_i\cdot b) $ for all $ b\in A $.

Proof By Proposition 3.2, $ A_Q/(A_Q)^{\text {co}H_Q} $ is a Hopf dense Galois extension over the field $ Q $. By Lemma 3.6, $ R^i\Gamma_{A_Q}(A_Q) = 0 $ for $ i\leq2 $. Then [1, Theorem 3.10] insures that the natural map

$ \xi:A_Q\#H_Q^*\longrightarrow \operatorname {End}_{(A_Q)^{\text {co}H_Q}}(A_Q) $

is an isomorphism. By Lemma 3.5, we have $ (A_Q)^{\text {co}H_Q} = (A^{\text {co}H})_Q $. It follows $ \operatorname {End}_{(A_Q)^{\text {co}H_Q}}(A_Q) = \operatorname {End}_{A^{\text {co}H}}(A)_Q $. Moreover, since $ A_Q\#H_Q^* = (A\#H^*)_Q $, it follows that $ \xi = \psi_Q:(A\#H^*)_Q\longrightarrow \operatorname {End}_{A^{\text {co}H}}(A)_Q $. We next show that $ \psi $ is a monomorphism. Let $ K = \ker \psi $ and $ M = \text{coker} \psi $. Then $ K_Q = \ker \xi = 0 $ and $ M_Q = \text{coker} \xi = 0 $. Since $ A $ is projective over $ R $ and $ H $ is $ R $-free, it follows that $ A\#H^* $ is projective over $ R $. Since $ R $ is a domain, $ A\#H^* $ is $ R $-torsion free. Hence $ K $ is $ R $-torsion free, which implies $ K = 0 $. Therefore $ \psi $ is injective. Moreover, since $ M_Q = 0 $, it follows that for each $ f\in\operatorname {End}_{A^{\text {co}H}}(A) $, there is an element $ 0\neq r\in R $ such that $ rf $ lies in the image of $ \psi $, that is $ rf = \psi(\sum\limits_{i = 1}^na_i\#\alpha_i) $ for some $ \sum\limits_{i = 1}^na_i\#\alpha_i\in A\#H^* $. Hence $ rf(b) = \sum\limits_{i = 1}^na_i(\alpha_i\cdot b) $ for all $ b\in A $.

In this section, $ R $ is a noetherian commutative domain of characteristic zero, and $ \mathbb{k} $ is an algebraic closed field containing $ R $ as a subring. $ H $ is an $ R $-Hopf algebra which is a finitely generated free $ R $-module. The filtration of a filtered $ R $-algebra $ A $ is an ascending filtration

$ 0 \subseteq F_0A \subseteq F_1A \subseteq \cdots \subseteq F_i A \subseteq \cdots, \ i \in \mathbb{N}. $

We call an $ R $-algebra $ A $ is almost commutative if $ A $ is a filtered $ R $-algebra and the associated graded algebra $ gr (A) $ is a graded commutative algebra. Similar to equation (3.1), we will write

$ H^*_\mathbb{k} = \operatorname {Hom}_R (H, R) \otimes_R \mathbb{k} \cong \operatorname {Hom}_\mathbb{k} (H \otimes_R \mathbb{k}, \mathbb{k}) $

for simplicity.

Lemma 4.8 Let $ B = B_0\oplus B_1\oplus\cdots $ be a graded $ R $-algebra which is a commutative domain and is projective over $ R $. Let $ \rho:B\to B\otimes_R H $ be a right $ H $-coaction on $ B $ which preserves the gradings. If $ B/B^{\text {co}H} $ is a Hopf dense Galois extension, then $ H^*_\mathbb{k} $ is isomorphic to a group algebra.

Proof We write $ B_\mathbb{k} = B\otimes_R\mathbb{k} $ and $ H_\mathbb{k} = H\otimes_R\mathbb{k} $. Applying $ -\otimes_R\mathbb{k} $ to the right coaction $ \rho:B\to B\otimes_RH $, we obtain a coaction $ \rho_\mathbb{k}:B_\mathbb{k}\to B_\mathbb{k}\otimes_\mathbb{k} H_k $. Consider the canonical map $ \beta_\mathbb{k}:B_\mathbb{k}\otimes_{B^{coH_\mathbb{k}}} B_\mathbb{k}\longrightarrow B_\mathbb{k} \otimes_\mathbb{k} H_\mathbb{k} $. Since $ B $ is commutative, $ \beta_\mathbb{k} $ is indeed an algebra homomorphism, where we view $ B_\mathbb{k} \otimes_\mathbb{k} H_\mathbb{k} $ as the algebra by the usual multiplication of tensor products of algebras. The same proof of Proposition 3.2 shows that $ B_\mathbb{k}/(B_\mathbb{k})^{coH_\mathbb{k}} $ is a Hopf dense Galois extension, then the cokernel of $ \beta_\mathbb{k} $ is finite dimensional over $ \mathbb{k} $. Then there is an integer $ n\ge0 $ such that $ (\oplus_{i\ge n}B_i)_\mathbb{k}\otimes_\mathbb{k} H_\mathbb{k}\subseteq\operatorname {im} \beta_\mathbb{k} $. Since by assumption $ B $ is commutative, which implies $ B_\mathbb{k}\otimes_{B^{coH_\mathbb{k}}} B_\mathbb{k} $ is commutative, and thus $ \operatorname {im} \beta_\mathbb{k} $ is commutative. For $ g, h\in H $, taking nonzero elements $ a, b\in (\oplus_{i\ge n}B_i)_\mathbb{k} $, then $ (a\otimes_\mathbb{k} g), (b\otimes_\mathbb{k} h) \in \operatorname {im} \beta_\mathbb{k} $, which impies $ (a\otimes_\mathbb{k} g)(b\otimes_\mathbb{k} h) = (b\otimes_\mathbb{k} h)(a\otimes_\mathbb{k} g) $. Then $ ab\otimes_\mathbb{k} gh = ba\otimes_\mathbb{k} hg = ab\otimes_\mathbb{k} hg $. Since $ B $ is a domain and $ B $ is projective over $ R $, $ ab\neq 0 $. Hence we have $ gh = hg $, that is, $ H_\mathbb{k} $ is commutative. Since $ H $ is finitely generated as an $ R $-module, $ H_\mathbb{k} $ is finite dimensional. Therefore the dual Hopf algebra $ H_\mathbb{k}^* $ is cocommutative. Since $ \mathbb{k} $ is algebraic closed with characteristic zero, $ H_\mathbb{k}^* $ is isomorphic to a group algebra.

Let $ B $ be a filtered $ R $-algebra. Let $ M $ be a filtered right $ B $-module and let $ N $ be a left filtered $ B $-module. The tensor product $ M\otimes_BN $ has an induced filtration defined by $ F_n(M\otimes_BN) $ to be the abelian subgroup of $ M\otimes_B N $ generated by elements $ x\otimes y $ for all $ x\in F_iM $ and $ y\in F_jN $ such that $ i+j = n $. There is a graded epimorphism (cf. [8, §Chapter I])

$ \begin{equation} \varphi_{M, N}: gr (M) \otimes_{gr (B)} gr (N) \longrightarrow gr (M\otimes_B N), \ \overline{x} \otimes \overline{y} \mapsto \overline{x \otimes y}, \end{equation} $

(4.1)

where $ x\in F_iM\setminus F_{i-1}M $, $ y\in F_jN\setminus F_{j-1}N $ and $ \overline{x}, \overline{y} $ are corresponding elements in the associated graded modules, similarly $ \overline{x\otimes y} $ is the corresponding element in the graded abelian group associated to $ M\otimes_B N $.

Suppose that there is a right $ H $-coaction $ \rho:B\to B\otimes_RH $ which preserves the filtration, where the filtration of $ B \otimes_R H $ is induced by the filtration of $ B $. Then the induced map

$ gr (\rho) : gr (B) \longrightarrow gr (B) \otimes_R H $

is a right $ H $-coaction on the associated graded algebra $ gr (B) $. Then the filtration of $ B $ induces a filtration on $ B^{\text {co}H} $. Associated to this filtration, there is a graded algebra $ gr (B^{\text {co}H}) $. Then $ gr (B^{\text {co}H}) $ is a graded subalgebra of $ (gr (B))^{\text {co}H} $. In general, $ gr (B^{\text {co}H}) $ is not equal to $ (gr (B))^{\text {co}H} $.

Let $ X $ and $ Y $ be filtered $ R $-modules. An $ R $-module homomorphism $ f:X\to Y $ is called a strict filtered map [8] if $ f $ preserves the filtration and $ F_nY\cap \operatorname {im} f = f(F_nX) $ for all $ n $.

Lemma 4.9 Keep the notations as above. If $ B/B^{\text {co}H} $ is a and the canonical map $ \beta: B\otimes_{B^{\text {co}H}}B\to B\otimes_R H $ is strict, then $ gr (B)/(gr (B))^{\text {co}H} $ is a Hopf dense Galois extension.

Proof Let $ gr(\rho): gr (B) \to gr (B) \otimes_R H $ be the induced $ H $-coaction on $ gr(B) $. Let

$ \beta_{gr}: gr (B) \otimes_{(gr (B))^{\text {co}H}}gr (B) \to gr (B) \otimes_R H, \ a\otimes b\mapsto (a\otimes1)(gr(\rho)(b)) $

be the canonical map associated to $ gr (\rho) $. Denote $ K = \text{coker} \beta $. Then $ K $ has a natural filtration inherits from $ B\otimes_RH $. Since $ \beta $ is strict, by [8, Theorem 4.2.4, Chapter I], we have an exact sequence

$gr(B{{\otimes }_{{{B}^{\text{co}H}}}}B)\overset{gr(\beta )}{\mathop{\to }}\, gr(B{{\otimes }_{R}}H)\to gr(K)\to 0. $

By equation (4.1), the map $ \varphi_{B, B}:gr (B) \otimes_{gr (B^{\text {co}H})}gr (B) \longrightarrow gr(B\otimes_{B^{\text {co}H}}B) $ is an epimorphism. Note that $ gr (B\otimes_RH) = gr (B) \otimes_RH $, we have the following commutative diagram

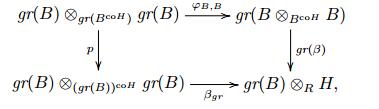(4.2)

where $ p $ is an epimorphism induced by the fact that $ gr(B^{\text {co}H}) $ is a graded subalgebra of $ (gr (B))^{\text {co}H} $. Since $ \varphi_{B, B} $ and $ p $ are both epic, we have $ \text{coker} \beta_{gr} = \text{coker} gr (\beta) \cong gr (K) $. By assumption, $ B/B^{\text {co}H} $ is a Hopf dense Galois extension, thus $ K_Q $ is finite dimensional over $ Q $. Then $ (gr (K))_Q = gr (K_Q) $ is also finite dimensional over $ Q $. Therefore $ gr (B)/(gr (B))^{\text {co}H} $ is a Hopf dense Galois extension.

Theorem 4.10 Let $ A $ be an almost commutative $ R $-algebra such that $ gr (A) $ is a domain. Assume that $ A $ is a right $ H $-comodule algebra such that the right $ H $-coaction preserves the filtration. If $ A/A^{\text {co}H} $ is a Hopf dense Galois extension and the canonical map $ \beta : A\otimes_{A^{\text {co}H}} A\to A\otimes_RH $ is strict, then $ H^*_\mathbb{k} $ is isomorphic to a group algebra over $ \mathbb{k} $.

Proof As before, we write $ A_\mathbb{k} = A\otimes_R\mathbb{k} $ and $ H_\mathbb{k} = H\otimes_R\mathbb{k} $. Since $ A $ is a filtered $ R $-algebra, $ A_\mathbb{k} $ is also a filtered $ \mathbb{k} $-algebra with the obvious induced filtration. Since the right $ H $-coaction preserves the filtration, it induces a right $ H $-coaction on the associated graded algebra $ gr (A) $. Applying the functor $ -\otimes_R\mathbb{k} $ to the right $ H $-coaction $ \rho: A\to A\otimes_RH $, we obtain that $ A_\mathbb{k} $ is a right $ H_\mathbb{k} $-comodule algebra and $ A_\mathbb{k}/(A_\mathbb{k})^{coH_\mathbb{k}} $ is a Hopf dense Galois extension. Moreover, since $ \beta $ is strict, the induced canonical map $ \beta_\mathbb{k} $ is also a strict filtered map. By Lemma 4.1, $ gr (A_\mathbb{k})/(gr (A_\mathbb{k}))^{coH_\mathbb{k}} $ is a Hopf dense Galois extension. Since $ A $ is almost commutative, $ gr (A) $ is a commutative domain. Then $ gr (A_\mathbb{k}) = gr (A) \otimes_R \mathbb{k} $ is a commutative domain over $ \mathbb{k} $. By Lemma 4.8, $ H^*_\mathbb{k} $ is a group algebra.

For a filtered algebra $ A $ and a filtration preserving right $ H $-coaction, the canonical map

$ \beta : A\otimes_{A^{\text {co}H}} A\to A\otimes_RH $

may be not a strict map. Hence the associated graded algebra $ gr (A) $ may not be a Hopf dense Galois extension over $ (gr (A))^{\text {co}H} $. Some further discussions will be given in the next section.

In this section, $ \mathbb{k} $ is an algebraically closed field of characteristic zero. All the algebras and modules in this section are over $ \mathbb{k} $. Let $ H $ be a finite dimensional Hopf algebra.

The next result is a direct consequence of [2, Proposition 3.6] if $ A $ is noetherian and $ H $ is semisimple. We give a direct proof and drop the assumptions in [2, Proposition 3.6].

Proposition 5.3 Let $ A $ be a filtered algebra with an ascending filtration

$ 0\subseteq F_0A\subseteq F_1A\subseteq \cdots \subseteq F_i A \subseteq \cdots, \ i \in \mathbb{N} $

such that $ F_iA $ is finite dimensional for all $ i\ge0 $. Assume that $ A $ is a right $ H $-comodule algebra and the coaction preserving the filtration. If the associated graded algebra $ gr (A) $ is a Hopf dense Galois extension over $ (gr (A))^{\text {co}H} $, then $ A/A^{\text {co}H} $ is a Hopf dense Galois extension.

Proof Let $ \beta : A\otimes_{A^{\text {co}H}} A\to A\otimes_\mathbb{k} H $ be the canonical map. Similar to the diagram (4.2), we have the following commutative diagram

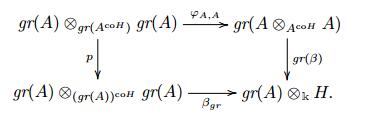(5.1)

Since $ gr (A)/(gr (A))^{\text {co}H} $ is a Hopf dense Galois extension, which is to say that $ \text{coker} \beta_{gr} $ is finite dimensional. It follows that there is a positive number $ n $ such that for all $ k\ge n $, we have

$ \beta_{gr}(gr (A) \otimes_{(gr (A))^{\text {co}H}} gr (A))_k = (F_kA/F_{k-1}A) \otimes_\mathbb{k} H. $

We claim that $ \beta(F_k(A\otimes_{A^{\text {co}H}}A))+ F_{n-1}A \otimes_{\mathbb{k}} H = F_kA\otimes_\mathbb{k} H $ for all $ k\ge n $. By the commutative diagram (5.1), for every $ x\in F_nA \otimes_\mathbb{k} H $, there is an element $ y\in F_n(A\otimes_{A^{\text {co}H}} A) $ such that $ \beta(y)+z = x $ for some $ z\in F_{n-1}A\otimes_\mathbb{k} H $. Hence $ \beta(F_n(A\otimes_{A^{\text {co}H}}A))+ F_{n-1}\otimes_\mathbb{k} H = F_nA\otimes_\mathbb{k} H $. Now assume that $ \beta(F_i(A\otimes_{A^{\text {co}H}}A))+ F_{n-1}A\otimes_\mathbb{k} H = F_iA\otimes_\mathbb{k} H $ for $ i \ge n $. By the commutative diagram (5.1), we have $ \beta(F_{i+1}(A\otimes_{A^{\text {co}H}}A))+ F_{i}A\otimes_\mathbb{k} H = F_{i+1}A\otimes_\mathbb{k} H $. Then

$ \begin{array}{ccl} F_{i+1}A\otimes_\mathbb{k} H& = &\beta(F_{i+1}(A\otimes_{A^{\text {co}H}}A))+ \beta(F_{i}(A\otimes_{A^{\text {co}H}}A))+F_{n-1}A\otimes_\mathbb{k} H\\ & = &\beta(F_{i+1}(A\otimes_{A^{\text {co}H}}A))+F_{n-1}A\otimes_\mathbb{k} H. \end{array} $

Hence we have $ \dim((A\otimes_\mathbb{k} H)/\operatorname {im} \beta)\leq \dim (F_{n-1}A\otimes_\mathbb{k} H)<\infty $. Therefore, $ A/A^{\text {co}H} $ is a Hopf dense Galois extension.

Combined with Lemma 4.9, we have the following corollary.

Corollary 5.11 With the same conditions in Proposition 5.3, if in addition the canonical map $ \beta : A \otimes_{A^{\text {co}H}} A \rightarrow A \otimes_\mathbb{k} H $ is strict, then $ A / A^{\text {co}H} $ is a Hopf dense Galois extension if and only if $ gr (A)/(gr (A))^{\text {co}H} $ is a Hopf dense Galois extension.

Let $ \mathfrak{g} $ be a finite dimensional Lie algebra, and let $ f:\mathfrak{g}\times\mathfrak{g}\to \mathbb{k} $ be a $ 2 $-cocycle, that is, for every $ x, y, z\in \mathfrak{g} $, $ f(x, x) = 0, \ f(x, [y, z])+f(z, [x, y])+f(y, [z, x]) = 0. $ Then a Sridharan enveloping algebra [9] of $ \mathfrak{g} $ is defined to be the associative algebra

$ U_f(\mathfrak{g}) = T(\mathfrak{g})/I, $

where $ T(\mathfrak{g}) $ is the tensor algebra of $ \mathfrak{g} $ over $ \mathbb{k} $ and $ I $ is the ideal of $ T(\mathfrak{g}) $ generated by elements

$ x\otimes y-y\otimes x-[x, y]-f(x, y)\ \text{ for all } x, y\in \mathfrak{g}. $

Assume that $ \{x_1, \dots, x_n\} $ is an $ R $-basis of $ \mathfrak{g} $. Then $ U_f(\mathfrak{g}) $ is a free $ R $-module and it has a basis $ \{x_1^{i_1}x_2^{x_2}\cdots x_n^{i_n}|i_1, i_2, \dots, i_n\ge 0\} $ (cf. [9, Theorem 2.6]). And $ U_f(\mathfrak{g}) $ is a filtered algebra with an ascending filtration defined by

$ F_kU_f(\mathfrak{g}) = \text{span}\{x_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}|i_1+i_2+\cdots+i_n\leq k\} $

for all $ k\ge0 $. The associated graded algebra of $ U_f(\mathfrak{g}) $ is the commutative polynomial ring $ \mathbb{k}[x_1, \dots, x_n] $.

Suppose that there is a right $ H $-coaction $ \rho_\mathfrak{g}:U_f(\mathfrak{g})\to U_f(\mathfrak{g})\otimes_\mathbb{k} H $ which preserves the filtration defined as above. Then the associated graded map $ gr(\rho_\mathfrak{g}):grU_f(\mathfrak{g})\to grU_f(\mathfrak{g})\otimes_\mathbb{k} H $ is a right $ H $-coaction on $ grU_f(\mathfrak{g}) $.

Corollary 5.12 With the notions as above, if $ grU_f(\mathfrak{g}) $ is a Hopf dense Galois extension over $ (grU_f(\mathfrak{g}))^{\text {co}H} $, then $ U_f(\mathfrak{g}) $ is a Hopf dense Galois extension over $ U_f(\mathfrak{g})^{\text {co}H} $ and $ H^* $ is isomorphic to a group algebra.

Proof The first part follows from Proposition 5.3. The second part follows from Lemma 4.8 since $ grU_f(\mathfrak{g})\cong \mathbb{k}[x_1, \dots, x_n] $.

As we know, a right $ H $-coaction on an algebra $ A $ is equivalent to a left $ H $-action on $ A $. Moreover, we have $ A^{\text {co}H} = A^H $, where $ A^H = \{a\in A|ha = \varepsilon(h)a, \ \text{for all} \ h\in H\} $. Hence we may rewrite Corollary5.12 in the Hopf action version.

Corollary 5.13 Suppose that $ H $ acts on a Sridharan enveloping algebra $ U_f(\mathfrak{g}) $. If the $ H $-action preserves the filtration of $ U_f(\mathfrak{g}) $ and $ grU_f(\mathfrak{g}) $ is a right $ H^* $-Hopf dense Galois extension over $ (grU_f(\mathfrak{g}))^H $, then $ U_f(\mathfrak{g}) $ is a right $ H^* $-Hopf dense Galois extension over $ U_f(\mathfrak{g})^H $, and $ H $ is isomorphic to a group algebra.