An algebra $L$ is said to be subdirectly irreducible (s.i) if it has a smallest non-trivial congruence; i.e., a congruence $\alpha $, such that $\theta \geq \alpha $ for all $\theta \in {\rm Con}L $ with $\theta \neq \omega .$ A particularly important case of a subdirectly irreducible algebra is a simple algebra, namely, one for which the lattice of congruence is the two-element chain $\{\omega , \iota \}$. Associated with the notion of a subdirectly irreducible algebra is that of a finitely subdirectly irreducible (f.s.i) algebra, this being defined as an algebra in which the intersection of two non-trivial principal congruences is non-trivial. Clearly, every s.i. algebra is f.s.i. algebra and f.s.i. semilattices, distributive lattices and Boolean algebras are s.i. Many algebras arising in logic have (distributive) lattice reducts and share the same property; for example, De Morgan algebras [1], the Post algebras of order $n$, the $n$-valued Lukasiewicz algebras [2] and demi-$p$-lattices [3]. In this paper, we consider the class of bounded distributive lattices endowed with an unary operation, which is an endomorphism $f$ with $f(0)=0, f(1)=1$ (the class will be denoted by $ {\bf{eD}}$), characterise finitely subdirectly irreducible algebras and the subdirectly irreducible algebras in $ {\bf{eD}}$.

Let $(L, f)\in $ $ {\bf{eD}}$ and let $f^{0}=id $ and define $f^{n}$ recursively by $f^{n}(x)=f(f^{n-1}(x))$ for $n\geq 1$, then for $p, q\in \mathbb{N} $ with $p>q\geq 0$, we define the subclass ${\bf{e}}_{p, q}{\bf{D}}$ of $ {\bf{eD}}$ by adjoining the equation $f^{p}=f^{q}$. It follows that the smallest nontrivial subclass ${\bf{e}}_{p, q}{\bf{D}}$ is the class ${\bf{e}}_{1, 0}{\bf{D}}$, which is determined by the equation $f=id$. We define ${\bf{e}}_{2, 0}{\bf{D}}$ to be the class of symmetric extended distributive lattices, see [4].

A congruence on $L$ is an equivalence relation that has the substitution property for both the lattice operations and for the unary operation $f$. It follows that every congruence is in particular a lattice congruence and it is essential to distinguish these two types. In order to do so, we shall use the subscript 'lat' to denote a lattice congruence.

Lemma 2.1 (see [5]) Let $(L, f)\in $ $ {\bf{eD}}$. If $a, b\in L$ with $a\leq b$ in $L$, then

$ \theta (a,b) = \mathop \vee \limits_{n \ge 0} {\theta _{{\rm{lat}}}}({f^n}(a),{f^n}(b)). $

Corollary 2.1 Let $(L, f)\in $ ${\bf{e}}_{2, 0}{\bf{D}}$. Then

$ \theta (a, b)=\theta _{{\rm lat}}(a, b)\vee \theta _{{\rm lat}}(f(a), f(b)). $

For an algebra $(L;f)\in $ $ {\bf{eD}}$, consider now, for every $n\in \mathbb{N}$, the relation $\Phi _{n}$ on $L$ defined by $(x, y)\in \Phi _{n}\Leftrightarrow f^{n}(x)=f^{n}(y).$

It is clear that $\Phi _{n}$ is a congruence on $L$. Moveover, the subset $f^{n}(L)=\{f^{n}(x)|x\in L\}$ is a subalgebra of $L.$

We now consider some basic results concerning these congruences. Of especial importance in this is the congruence $ \Phi \omega = \mathop \vee \limits_{i \ge 0} {\Phi _i}. $

For every non-trivial algebra $(L;f)\in $ $ {\bf{eD}}$, it is clear that we have

$ \omega =\Phi _{0}\leq \Phi _{1}\leq \Phi _{2} \leq\cdots \leq \Phi _{i} \leq \Phi _{i+1} \leq \cdots \leq \Phi _{\omega} <\iota $

and with $\leq $ meaning "is a subalgebra of",

$ \{0, 1\} \leq\ldots\leq f^{i+1}(L)\leq f^{i}(L)\leq \ldots \leq f(L)\leq f^{0}(L)=L. $

It is readily seen that $[x]\Phi _{i}\rightarrow f^{i}(x)$ describes an algebra isomorphism in $ {\bf{eD}}$. We shall denote by writing $L/\Phi _{i}\backsimeq f^{i}(L).$

The following result is therefore clear.

Lemma 2.2 If $(L;f)\in $ ${\bf{e}}_{p, q}{\bf{D}}$, then, for $n\leq q, $

$ L/\Phi _{n}\backsimeq f^{n}(L)\in {\bf{e}}_{p, q-n}{\bf{D}} . $

The following two lemmas are an extension to $ {\bf{eD}}$-algebras of Blyth for Ockham algebras ^[6].

Lemma 2.3 If $(L;f)\in $ ${\bf{e}}_{p, q}{\bf{D}}$, then

$ \omega =\Phi _{0}\leq \Phi _{1}\leq \cdots \leq \Phi _{q} = \Phi _{q+1} = \cdots = \Phi _{\omega}. $

Moreover, if $(L;f)$ belongs to the subclass ${\bf{e}}_{p, q}{\bf{D}}$, then each of the above is equivalent to $(L;f)\in $ ${\bf{e}}_{p-q, 0}{\bf{D}}$.

Lemma 2.4 If $(L;f)\in $ ${\bf{e}}_{p, q}{\bf{D}}$, $a, b\in L$ are such that $a\prec b$ and $f(a)=f(b)$ then $\theta (a, b)$ is an atom of Con$L$.

Given an algebra $(L;f)\in $ $ {\bf{eD}}$, consider now for each $i\geq 1$ the subset

$ T_{i}(L)=\{x\in L|f^{i}(x)=x\}. $

In particular, $T_{1}(L)$ is the set of fixed points of $f$. Of course, $T_{1}(L)$ is never empty, for it clearly contains $0$ and $1$. It is readily seen that every subset $T_{n}(L)$ is a subalgebra of $L$; in fact $T_{n}(L)$ is the largest ${\bf{e}}_{n, 0}{\bf{D}}$-subalgebra of $L$.

Consider now the subset

$ T(L)=\{x\in L| \ \mbox{there exists a positive integer}\ \ m_{x} \ \mbox{such that}\ \ f^{m_{x}}(x)=x\}. $

Given $x, y\in T(L), $ let $m=lcm\{m_{x}, m_{y}\}.$ Then, $m$ being positive integer, we have

$ f^{m}(x\vee y)=f^{m}(x)\vee f^{m}(y)=x\vee y, $

and similarly $f^{m}(x\wedge y)=x\wedge y.$ Since $x\in T(L)$ clearly implies $f(x)\in T(L)$, it follows that $T(L)$ is also a subalgebra of $L$.

Theorem 3.1 Let $(L;f)\in $ $ {\bf{eD}}$ be finitely subdirectly irreducible. Then $T_{1}(L)=\{0, 1\}.$

Proof Suppose that $T_{1}(L)$ contains at least three elements. Then it contains a 3-element chain $0<a<1$. Then, by Lemma 2.1, we have $\theta (0, a)=\theta _{{\rm lat}}(0, a)$ and $\theta (a, 1)=\theta _{{\rm lat}}(a, 1), $ whence we have the contradiction $\theta (0, a)\wedge \theta (a, 1)=\omega .$

Consider now the particular case where $L$ is a finitely subdirectly irreducible symmetry extended distributive lattice.

Lemma 3.1 Let $L\in $ ${\bf{e}}_{2, 0}{\bf{D}}$. Then for $x\in L\setminus \{0, 1\}$, either $x||f(x)$, or $x=f(x)$.

Corollary 3.1 Let $L\in $ ${\bf{e}}_{2, 0}{\bf{D}}$ be finitely subdirectly irreducible and $|L|\geq 2$. Then for $x\in L \setminus \{0, 1\}$, $x||f(x)$.

Proof If $x\in L\setminus \{0, 1\}$, then $x\neq f(x)$ according to Theorem 3.1 and so $x||f(x)$ by Lemma 3.1.

Theorem 3.2 In the class ${\bf{e}}_{2, 0}{\bf{D}}$ of symmetric extended distributive lattices there are only two (finitely) subdirectly irreducible algebras, each of which is simple, namely, the algebras.

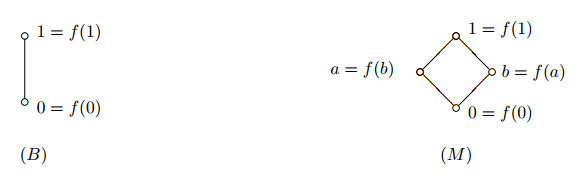Proof If $|L|=2$, then $L=\{0, 1\}$. If $|L|=3$, let $L=\{0, a, 1\}$, then $a\not\in \{0, 1\}$. We have $a||f(a)$ according to Corollary 3.1 and so $|L|\neq 3$, which is absurd. If $|L|=4$, let $L=\{0, a, b, 1\}$, then $a, b\not\in \{0, 1\}$ and $a||f(a)$, $b||f(b)$. Thus $f(a)=b$, $f(b)=a$. Thus $L$ is $M$ in the above figures. If $|L|\geq 5$, then $L$ has $5$ distinct points $0, a, b, c, 1$. If $a\wedge b\neq 0$, then $f(a\wedge b)\neq 0$ and $a\wedge b\wedge f(a\wedge b)=0, (a\wedge b)\vee f(a\wedge b)=1$ by Theorem 3.1. Since $a\wedge f(a)=0$ and $b\wedge f(b)=0, (a\wedge b)\wedge f(a\vee b)=0$ and $(a\wedge b)\vee f(a\vee b)=1$, $f(a\vee b)=f(a\wedge b)$ and so $f(a)=f(b), a=b$, a contradiction. Thus $a\wedge b=0$ and so $a\wedge (f(a)\vee b)=0, a\vee (f(a)\vee b)=1$ and therefore

$ f(a)\vee b=f(a), {\rm i.e.}, f(a)\geq b. $

Likely, $b\wedge (f(b)\vee a)=0, b\vee (f(b)\vee a)=1$ and therefore $f(b)\vee a=f(b)$ and so $f(b)\geq a$ and also $b\geq f(a)$. Hence we have $f(a)=b$ and so $a\vee b=1$. Also, $a\wedge c=0, a\vee c=1$. By distributive $b=c, $ a contradiction.

Thus if $L$ is a finitely subdirectly irreducible symmetry extended distributive lattice, then $L$ is only of the two kinds in the above figures.

It is readily seen that for these we have Con$B=$Con$M\simeq 2.$ So these algebras are indeed subdirectly irreducible; in fact, they are simple.

Theorem 3.3 If $L\in $ $ {\bf{eD}}$ is such that $T_{1}(L)=\{0, 1\}$ and if $a, b\in T(L)$ are such that $a<b$ then $\theta (a, b)=\iota .$

Proof For every $x\in T(L)$, let $m_{x}$ be the least positive integer such that $f^{m_{x}}(x)=x$. Consider the elements

$ \alpha (x)=x\wedge f(x)\wedge \cdots \wedge f^{m_{x}-1}(x), \beta (x)=x\vee f(x)\vee \cdots \vee f^{m_{x}-1}(x). $

Observe that $f(\alpha (x))=\alpha (x)$ and $f(\beta (x))=\beta (x)$, so $\alpha (x), \beta (x)\in T_{1}(L)=\{0, 1\}.$ Now, let $a, b\in T(L)$ be such that $a<b.$ Consider the sublattice $A$ that is generated by

$ \{f^{i}(a), f^{j}(b)|0\leq i\leq m_{a}-1, 0\leq j\leq m_{b}-1\}. $

Clearly, $A$ is finite with the smallest element $\alpha (a)=0$ and the greatest element $\beta (b)=1$. Let $p$ be an atom of $A$ and since every atom of $A$ is of the form $ \mathop \wedge \limits_{i \ne j} {f^i}(a) $ for some $j$, it follows that $f(p)$ is also an atom of $A$ and $f^{m_{a}}(p)=p, $ and so

$ p\in T(L), \beta (p)=p\vee f(p)\vee \cdots \vee f^{m_{a}-1}(p)=1. $

Consequently, $A$ is boolean.

Let $c$ be an atom of $A$ with $c\not\leq a$ and $c\leq b$. Then $(0, c)=(a\wedge c, b\wedge c)\in \theta (a, b)$. It follows that $(0, f(c))\in \theta (a, b)$ and so $(0, \beta (c))\in \theta (a, b)$, i.e., $(0, 1)\in \theta (a, b)$ and therefore $\theta (a, b)=\iota $.

Theorem 3.4 For an algebra $L\in $ $ {\bf{eD}}$ the following are equivalent:

(1) $T_{1}(L)=\{0, 1\};$

(2) the subalgebra $T(L)$ is simple;

(3) all symmetric extended distributive sublattices of $L$ are simple.

Proof $(1)\Rightarrow (2)$ If (1) holds, then by Theorem 3.3 every non-trivial principal congruence on $T(L)$ coincides with $\iota $. Since every congruence is the supremum of the principal congruences that it contains, it follows that $T(L)$ is simple.

$(2)\Leftrightarrow (3)~~ T_{2}(L)$ is the largest symmetric extended distributive sublattice of $L$.

$(3)\Rightarrow (1)$ If (3) holds, then $T_{2}(L)$ is simple. But $T_{2}(L)$ is a symmetric extended distributive lattice and by Theorem 3.2 there are only two non-isomorphic simple symmetric extended distributive lattices, in each of which $T_{1}(T_{2}(L))=\{0, 1\}.$ Since $T_{2}(L)$ and $L$ have the same fixed points, (1) follows.

Theorem 3.5 If $L\in $ $ {\bf{eD}}$ is finitely subdirectly irreducible, then every $\Phi _{1}$-class in $L$ contains at most two elements.

Proof Suppose that a $\Phi _{1}$-class contains at least three elements. Then it contains a 3-element chain $x<y<z$ with $f(x)=f(y)=f(z)$. Then, by Lemma 2.1, we have $\theta (x, y)=\theta _{{\rm lat}}(x, y)$ and $\theta (y, z)=\theta _{{\rm lat}}(y, z), $ whence we have the contradiction $\theta (x, y)\wedge \theta (y, z)=\omega .$

Theorem 3.6 If $L\in $${\bf{e}}_{p, q}{\bf{D}}$ then the following statements are equivalent:

(1) $L$ is finitely subdirectly irreducible;

(2) $L$ is subdirectly irreducible.

Proof $(1)\Rightarrow (2)$ Since $L\in $${\bf{e}}_{p, q}{\bf{D}}$, for every $x\in L$, we have $f^{p}(x)=f^{q}(x)$. If $\Phi _{1}=\omega$, then $f$ is injective and $x=f^{p-q}(x)$, whence $x\in T(L)$. Thus $L=T(L)$ and it follows by Theorem 3.1 and Theorem 3.4 that $L$ is simple, hence subdirectly irreducible.

On the other hand, if $\Phi _{1}\neq \omega, $ then by Theorem 3.5 there is a two-element $\Phi _{1}$-class $\{a, b\}$, and by Lemma 2.4, $\theta (a, b)$ is an atom in the interval $[\omega , \Phi _{1}]$ of Con$L.$ If now $\alpha \in $ Con$L $ with $\alpha \neq \omega$ then, since $\alpha$ is the supremum of the non-trivial principal congruences which it contains and since Con$L$ satisfies the infinite distributive law $\beta \wedge \vee \gamma _{i}=\vee (\beta \wedge \gamma _{i}), $ it follows by the hypothesis that $L$ is finitely subdirectly irreducible that $\theta (a, b)\wedge \alpha =\theta (a, b)$ and hence $\theta (a, b)\leq \alpha .$ Thus $\theta (a, b)$ is the smallest non-trivial congruence on $L, $ so $L$ is subdirectly irreducible.

$(2)\Rightarrow (1)$ This is clear.

The following theorem is an extension to $ {\bf{eD}}$-algebras of Blyth for Ockham algebras, see [6].

Theorem 3.7 $L\in $ ${\bf{e}}_{p, q}{\bf{D}}$ is subdirectly irreducible if and only if Con $L$ reduces to the finite chain

$ \omega =\Phi _{0}\prec \Phi _{1}\prec \cdots \prec \Phi _{q} \prec l. $