1 Introduction
In this paper, assume that $E$ is a real Banach space with $E^*$ being its dual space. "$\rightarrow$" denotes strong convergence and $\langle x, f \rangle$ denotes the value of $f \in E^*$ at $x \in E.$
The normalized duality mapping $J: E \rightarrow 2^{E^*}$ is
defined by
| $
Jx : = \{f \in E^*: \langle x, f\rangle = \|x\|^2, ~ \|f\| = \|x\|\}, \quad\quad
x \in E.
$ |
If $E$ is uniformly smooth, then $J$ is norm-to-norm uniformly
continuous on each bounded subset in $E$[1].
For a mapping $A: D(A) \sqsubseteq E \rightarrow E, $ we use Fix(A) and $A^{-1}0$ to denote its fixed point set and the zero point set. That is, ${\rm{Fix}}(A) : = \{x\in D(A): Ax = x\}$ and $A^{-1}0: = \{x \in D(A): Ax = 0\}.$ The mapping $A : D(A) \sqsubseteq E \rightarrow E$ is said to be
(1) nonexpansive if
| $
\|Ax - Ay\| \leq \|x-y\|,\;\;\forall x, y \in
D(A);
$ |
(2) contraction with coefficient $k$ if there exists $0 < k < 1$ such that
| $
\|Ax - Ay\| \leq k \|x - y\|, \;\; \forall x, y \in D(A);
$ |
(3) accretive if for all $x, y \in D(A), $ there exists $j(x-y) \in J(x-y)$ such that
| $
\langle Ax - Ay, j(x-y)\rangle \geq 0;
$ |
(4) $m$-accretive if A is accretive and $R(I+\lambda A) = E$, $\forall \lambda >
0;$
(5) strongly positive operator with coefficient $\overline{\gamma} > 0$ [2] if $D(A) = E$ where $E$ is a real
smooth Banach space and
| $
\langle Ax,Jx\rangle \ge \bar \gamma {\left\| x \right\|^2},\;\;\forall x \in E.
$ |
In this case,
| $
\left\| {aI - bA} \right\| = \mathop {{\rm{sup}}}\limits_{\left\| x \right\| \le 1} \left| {\langle (aI - bA)x,Jx\rangle } \right|,
$ |
where $I$ is the identity mapping, $a \in
[0, 1]$ and $b \in [-1, 1]$;
(6) demiclosed at $p$ if whenever $\{x_n\}$ is a sequence in $D(A)$ such that $x_n \rightharpoonup x \in D(A)$ and $Ax_n \rightarrow p$ then $Ax =p$. Here '$\rightharpoonup$' denotes weak convergence in $E$.
If $A$ is accretive, then we can define, for each $r>0, $ a
single-valued mapping $J_r^A : R(I+rA)\rightarrow
D(A)$ by $J_r^A : = (I+rA)^{-1}, $ which is called the resolvent of
$A$ [1]. It is well known $J^A_r$ is non-expansive and $A^{-1}0 =
{\rm{Fix}}(J_r^A).$
Let $C$ be a nonempty, closed and convex subset of $E$ and $Q$ be a mapping of $E$ onto $C$. Then $Q$ is said to be sunny [3] if $Q(Q(x)+t(x-Q(x))) = Q(x), $ for all $x \in E$ and $t \geq 0.$
A mapping $Q$ of $E$ into $E$ is said to be a retraction[3] if $Q^2 = Q.$ If a mapping $Q$ is a retraction, then $Q(z) = z$ for every $z \in R(Q), $ where $R(Q)$ is the range of $Q.$
A subset $C$ of $E$ is said to be a sunny nonexpansive retract of $E$ [3] if there exists a sunny nonexpansive retraction of $E$ onto $C$ and it is called a nonexpansive retract of $E$ if there exists a nonexpansive retraction of $E$ onto $C.$
Finding the solution of the problem $0 \in A_ix$ $(i \in N^+)$ is one of hot topics in applied mathematics, where $A_i$ is accretive, since the
solutions correspond to the equilibrium
points of some evolution systems. Based on this reason, we shall first prove a new path convergence theorem and then present a new semi-implicit iterative scheme for
approximating the common zero of infinite m-accretive operators. Some new ideas and proof techniques can be found based on weaker restrictions than the recent works in [4-7].
Lemma 1.1[8] Assume $F$ is a strongly positive bounded operator with coefficient $\overline{\gamma} > 0$ on a real smooth Banach space $E$ and $0 < \rho \leq \|F\|^{-1}.$ Then $\|I-\rho F \| \leq 1- \rho \overline{\gamma}.$
Lemma 1.2[1] Let $E$ be a Banach space and $C$ be a
nonempty closed and convex subset of $E$. Let $f: C \rightarrow C$
be a contraction. Then $f$ has a unique fixed point $u \in C$.
Lemma 1.3[9] Let $E$ be a real uniformly convex Banach
space, $C$ be a nonempty closed and convex subset of $E$ and $B:
C \rightarrow E$ be a nonexpansive mapping such that ${\rm{Fix}}(B) \neq
\emptyset, $ then $I-B$ is demiclosed at zero.
Lemma 1.4[10] Let $E$ be a real strictly convex Banach
space and $C$ be its nonempty closed and convex subset. Let $B_m: C \rightarrow C$ be a nonexpansive mapping for each $m
\geq 1.$ Let $\{a_m\}$ be a real number sequence in (0, 1) such
that $\sum\limits_{m = 1}^{\infty}a_m = 1.$ Suppose that
$\bigcap\limits_{m=1}^{\infty}{\rm{Fix}}(B_m) \neq \emptyset.$ Then $\sum\limits_{m = 1}^{\infty}a_m B_m$ is nonexpansive with
| $
{\rm{Fix}}(\sum\limits_{m
= 1}^{\infty}a_mB_m) = \bigcap\limits_{m = 1}^{\infty}{\rm{Fix}}(B_m).
$ |
Lemma 1.5[11] In a real Banach space $E, $ the following
inequality holds
| $\|x+y\|^2 \leq \|x\|^2 + 2\langle y, j(x+y)\rangle, ~~\forall x, y \in E, j(x+y) \in J(x+y).
$ |
Lemma 1.6[6] Let $r, t >0.$ If $E$ is uniformly convex, then there exists a continuous strictly increasing and convex function $\varphi: R^+ \rightarrow R^+$
with $\varphi(0) = 0$ so that
| $
\|J_r^A x - J_r^A y \|^2 \leq \|x - y\|^2 - \varphi(\|(I-J_r^A)x - (I-J_r^A)y\|)
$ |
for all $x, y \in R(I+rA)$ with ${\rm{max}}\{\|x\|, \|y\|\}\leq t$, where $A: E \rightarrow E$ is m-accretive.
Lemma 1.7[12] Let $\{s_n\}$ be a real sequence that does not decrease at infinity, in the sense that there exists a subsequence $\{s_{n_k}\}$ so that $s_{n_k}\leq s_{n_k+1}, $ for all $k \geq 0.$ For every $n > n_0, $ define an integer sequence $\{\tau(n)\}$ as
| $
\tau(n) = {\rm{max}}\{n_0 \leq k \leq n : s_k < s_{k+1}\}.
$ |
Then $\tau(n) \rightarrow \infty$ as $n \rightarrow \infty$ and for all $n > n_0, $ ${\rm{max}}\{s_{\tau(n)}, s_n\} \leq s_{\tau(n)+1}.$
2 A New Path Theorem and A New Strong Convergence Theorem
Theorem 2.1 Suppose $E$ is a real uniformly smooth and uniformly
convex Banach space, $C$ is a nonempty, closed and convex sunny
nonexpansive retract of $E, $ and $Q_C$ is the sunny
nonexpansive retraction of $E$ onto $C.$ Let $f_i : E \rightarrow E$
be a contractive mapping with coefficient $k \in (0, 1)$ and $F_i:
E \rightarrow E$ be a strongly positive linear bounded operator
with coefficient $\overline{\gamma}, $ where $i \in N^+.$ Let $B : C \rightarrow C$ be
a nonexpansive mapping. Suppose $\{a_n\}$ and $\{b_n\}$ are real number sequences in (0, 1) with $\sum\limits_{i = 1}^{\infty}a_i = 1$
and $\sum\limits_{i = 1}^{\infty}b_i = 1$, $\sum\limits_{i = 1}^{\infty}\|f_i\| <+\infty$, $\sum\limits_{i = 1}^{\infty}b_i\|F_i\| <+\infty$, $0 <
\eta < \frac{\overline{\gamma}}{2k}$ and ${\rm{Fix}}(B) \neq \emptyset.$
If for $\forall t \in (0, 1), $ define $W_t : E \rightarrow E$ by
| $
W_t x : = t \eta \sum\limits_{i = 1}^{\infty}a_i f_i(x) + (I-t \sum\limits_{i = 1}^{\infty}b_i F_i)BQ_Cx,
$ |
(2.1) |
then $W_t$ has a fixed point $x_t, $ for each $0 < t \leq
(\sum\limits_{i = 1}^{\infty}b_i\|F_i\|)^{-1}, $ which is convergent strongly to the fixed point of
$B$, as $t \rightarrow 0.$ That is, $\mathop {{\rm{lim}}}\limits_{t \to 0} {x_t} = {p_0} \in {\rm{Fix}}(B).$ Moreover, $p_0$ is the unique solution of the following variational
inequality: for $\forall z \in {\rm{Fix}}(B), $
| $\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)p_0, J(p_0-z)\rangle \leq 0.
$ |
(2.2) |
Proof Step 1 $\sum\limits_{i = 1}^{\infty}b_i F_i : E \rightarrow E$ is a strongly positive linear bounded operator
with coefficient $\overline{\gamma}.$
It is easy to check $\sum\limits_{i = 1}^{\infty}b_i F_i : E \rightarrow E$ is linear bounded, so
we are left to show that $\sum\limits_{i = 1}^{\infty}b_i F_i : E \rightarrow E$ is strongly positive with coefficient $\overline{\gamma}.$
It follows from the property of $F_i$ that
| $
\langle \sum\limits_{i = 1}^{\infty}b_i F_ix, Jx\rangle = \sum\limits_{i = 1}^{\infty}b_i \langle F_ix, Jx\rangle
\geq \sum\limits_{i = 1}^{\infty}b_i\overline{\gamma}\|x\|^2= \overline{\gamma}\|x\|^2.
$ |
Thus $\sum\limits_{i = 1}^{\infty}b_i F_i : E \rightarrow E$ is a strongly positive operator
with coefficient $\overline{\gamma}$.
Step 2 $W_t$ is a contraction, for $0 < t <
(\sum\limits_{i = 1}^{\infty}b_i\|F_i\|)^{-1}$.
In fact, noticing lemma 1.1, $\sum\limits_{i = 1}^{\infty}a_i = 1$
and $\sum\limits_{i = 1}^{\infty}b_i = 1$, we have
| $
\|W_tx - W_ty\|\leq t\eta \sum\limits_{i = 1}^{\infty}a_i \|f_i(x) - f_i(y)\| + \|(I-t \sum\limits_{i = 1}^{\infty}b_i F_i)(BQ_Cx-BQ_Cy)\|
\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\leq kt\eta \|x - y\| + (1-t\overline{\gamma})\|x-y\| = [1-t(\overline{\gamma}-k\eta)]\|x - y\|,
$ |
which implies that $W_t$ is a contraction since $0 < \eta <
\frac{\overline{\gamma}}{2k}$. Then lemma 1.2 implies that $W_t$ has a unique fixed point, denoted
by $x_t, $ which uniquely solves the fixed point equation $x_t =
t\eta \sum\limits_{i = 1}^{\infty}a_i f_i(x_t) + (I-t \sum\limits_{i = 1}^{\infty}b_i F_i)BQ_Cx_t.$
Step 3 $\{x_t\}$ is bounded, for $t \in (0, (\sum\limits_{i = 1}^{\infty}b_i\|F_i\|)^{-1}).$ For $p \in {\rm{Fix}}(B)\subset C, $ we have $p = BQ_Cp, $ then
| $
\|x_t - p\| = \|(I-t \sum\limits_{i = 1}^{\infty}b_i F_i)(BQ_Cx_t-p) + t(\eta \sum\limits_{i = 1}^{\infty}a_i f_i(x_t) - \sum\limits_{i = 1}^{\infty}b_i F_ip)\|\\
\leq (1-t\overline{\gamma})\|x_t-p\| + t\|\eta \sum\limits_{i = 1}^{\infty}a_i(f_i(x_t)-f_i(p))\|+t\|\eta\sum\limits_{i = 1}^{\infty}a_if_i(p)-\sum\limits_{i = 1}^{\infty}b_iF_ip\|\\
\leq [1-t(\overline{\gamma}-k\eta)]\|x_t-p\|+t\|\eta\sum\limits_{i = 1}^{\infty}a_if_i(p)-\sum\limits_{i = 1}^{\infty}b_iF_ip\|.
$ |
This ensures that
| $
\|x_t - p\|\leq \frac{(\eta\sum\limits_{i = 1}^{\infty}\|f_i\|+\sum\limits_{i = 1}^{\infty}\|F_i\|)\|p\|}{\overline{\gamma}-k\eta}.
$ |
Thus $\{x_t\}$ is bounded, and then both $\{\sum\limits_{i = 1}^{\infty}a_if_i(x_t)\}$ and $\{\sum\limits_{i = 1}^{\infty}b_iF_iBQ_Cx_t\}$ are
bounded.
Step 4 $x_t - BQ_Cx_t \rightarrow 0, $ as $t
\rightarrow 0.$ From step 3, we have
| $
\|x_t - BQ_Cx_t\| = t
\|\eta \sum\limits_{i = 1}^{\infty}a_if_i(x_t)- \sum\limits_{i = 1}^{\infty}b_i F_iBQ_Cx_t\| \rightarrow 0,
$ |
as $t \rightarrow
0$.
Step 5 If variational inequality (2.2) has solutions, the
solution must be unique.
Suppose both $u_0\in {\rm{Fix}}(B)$ and $v_0 \in {\rm{Fix}}(B)$ are the
solutions of the variational inequality(2.2). Then we have
| $
\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)v_0, J(v_0-u_0)\rangle \leq 0
$ |
(2.3) |
and
| $
\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)u_0, J(u_0-v_0)\rangle \leq 0.
$ |
(2.4) |
Adding up (2.3) and (2.4), we obtain that
| $
\langle(\sum\limits_{i = 1}^{\infty}b_iF_i- \eta\sum\limits_{i = 1}^{\infty}a_i f_i)u_0 - (\sum\limits_{i = 1}^{\infty}b_iF_i- \eta\sum\limits_{i = 1}^{\infty}a_i f_i)v_0, J(u_0-v_0)\rangle \leq 0.
$ |
(2.5) |
Since
| $
\langle(\sum\limits_{i = 1}^{\infty}b_iF_i- \eta\sum\limits_{i = 1}^{\infty}a_i f_i)u_0 - (\sum\limits_{i = 1}^{\infty}b_iF_i- \eta\sum\limits_{i = 1}^{\infty}a_i f_i)v_0, J(u_0-v_0)\rangle\\
= \sum\limits_{i = 1}^{\infty}b_i\langle F_iu_0 - F_iv_0, J(u_0-v_0)\rangle - \eta \sum\limits_{i = 1}^{\infty}a_i\langle f_i(u_0) - f_i(v_0), J(u_0-v_0)\rangle\\
\geq \overline{\gamma}\|u_0-v_0\|^2 - k\eta \|u_0-v_0\|^2 = (\overline{\gamma}- k \eta)\|u_0-v_0\|^2,
$ |
then (2.5) implies that $u_0 = v_0.$
Step 6 $x_t \rightarrow p_0 \in {\rm{Fix}}(B), $ as $t \rightarrow 0, $ which satisfies the variational inequality (2.2).
Assume $t_n \rightarrow 0.$ Set $x_n : = x_{t_n}$ and defined $\mu : E \rightarrow \mathbb{R}$ by
$\mu(x) = LIM \|x_n - x\|^2, ~~x \in E, $
where LIM is the Banach limit on $\textit{l}^{\infty}$. Let
| $
K = \{ x \in E:\mu (x) = \mathop {{\rm{min}}}\limits_{x \in E} LIM{\left\| {{x_n} - x} \right\|^2}\} .
$ |
It is easily seen that $K$ is a nonempty closed convex bounded subset of $E$. Since $x_n - BQ_Cx_n \rightarrow 0, $ then for $x \in K, $
| $
\mu(BQ_Cx) = LIM \|x_n - BQ_Cx\|^2\leq LIM \|x_n - x\|^2 = \mu(x),
$ |
it follows that $BQ_C(K) \subset K; $ that is, $K$ is invariant under $BQ_C$. Since a uniformly smooth Banach space has the fixed point property for nonexpansive mappings, $BQ_C$ has a fixed point, say $p_0, $ in $K$. That is, $BQ_C p_0 = p_0 \in C$ which ensures that $p_0 = Bp_0$ from the definition of $B$ and then $p_0 \in {\rm{Fix}}(B).$ Since $p_0$ is also a minimizer of $\mu$ over $E$, it follows that, for $t \in (0, 1)$
| $
0 \leq \frac{\mu(p_0+\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0)-t\sum\limits_{i = 1}^{\infty}b_iF_ip_0)-\mu(p_0)}{t} \\
= LIM\frac{\|x_n-p_0-\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0)+t\sum\limits_{i = 1}^{\infty}b_iF_ip_0\|^2-\|x_n - p_0\|^2}{t} \\
= LIM \frac{ \langle x_n-p_0-\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0) +t
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_n-p_0-\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0) +t
\sum\limits_{i = 1}^{\infty}b_iF_ip_0)\rangle -\|x_n - p_0\|^2}{t}\\
= LIM \{\frac{ \langle x_n-p_0, J(x_n-p_0-\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0) +t\sum\limits_{i = 1}^{\infty}b_i
F_ip_0)\rangle - \|x_n - p_0\|^2} {t}\\+\frac{t\langle
\sum\limits_{i = 1}^{\infty}b_iF_ip_0-\eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0), J(x_n-p_0-\eta t \sum\limits_{i = 1}^{\infty}a_if_i(p_0) +t
\sum\limits_{i = 1}^{\infty}b_iF_ip_0)\rangle }{t}\}.
$ |
Since $E$ is uniformly smooth, then by letting $t \rightarrow 0, $ we find the two limits above can be interchanged and obtain
| $
LIM \langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0)-\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_n - p_0)\rangle \leq 0.
$ |
(2.6) |
Since $x_t - p_0 = t(\eta \sum\limits_{i = 1}^{\infty}a_if_i(x_t)-\sum\limits_{i = 1}^{\infty}b_iF_ip_0)+(I-t\sum\limits_{i = 1}^{\infty}b_iF_i)(BQ_Cx_t - p_0), $ then
| $
\|x_{t} - p_0\|^2 \\= t \langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(x_t) -
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_t-p_0)\rangle \\+ \langle (I-t\sum\limits_{i = 1}^{\infty}b_iF_i)(BQ_Cx_t-p_0), J(x_t-p_0)\rangle \\
\leq t \eta \langle \sum\limits_{i = 1}^{\infty}a_if_i(x_t) - \sum\limits_{i = 1}^{\infty}a_if_i(p_0), J(x_t-p_0)\rangle \\+t \langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0) -
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_t-p_0)\rangle \\+\| I -t\sum\limits_{i = 1}^{\infty}b_iF_i\|\|x_t -p_0\|^2\\
\leq [1-t(\overline{\gamma}-\eta k)]\|x_t -p_0\|^2\\+t \langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0) -
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_t-p_0)\rangle.
$ |
Therefore
| $
\|x_{t} - p_0\|^2 \leq \frac{1}{\overline{\gamma}-\eta k}\langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0) -
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_t-p_0)\rangle.
$ |
Hence by (2.6)
| $
LIM \|x_{n} - p_0\|^2 \leq \frac{1}{\overline{\gamma}-\eta k}LIM \langle \eta \sum\limits_{i = 1}^{\infty}a_if_i(p_0) -
\sum\limits_{i = 1}^{\infty}b_iF_ip_0, J(x_n-p_0)\rangle \leq 0,
$ |
which implies that $LIM \|x_{n} - p_0\|^2=0, $ and then there exists a subsequence which is still denoted by $\{x_n\}$ such that $x_n \rightarrow p_0.$
Next, we shall show that $p_0$ solves the variational inequality (2.2).
Since $x_t = t\eta \sum\limits_{i = 1}^{\infty}a_if_i(x_t)+(I-t\sum\limits_{i = 1}^{\infty}b_i F_i)BQ_Cx_t, $ then
| $
(\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)x_t = -\frac{1}{t}(I-t\sum\limits_{i = 1}^{\infty}b_i F_i)(I-BQ_C)x_t.
$ |
$\forall z \in {\rm{Fix}}(B), $ we have
| $
\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)x_t, J(x_t - z)\rangle\\ = -\frac{1}{t}\langle (I-t\sum\limits_{i = 1}^{\infty}b_i F_i)(I-BQ_C)x_t, J(x_t-z)\rangle\\
= -\frac{1}{t} \langle (I-BQ_C)x_t-(I-BQ_C)z, J(x_t-z)\rangle \\+ \langle \sum\limits_{i = 1}^{\infty}b_i F_i(I-BQ_C)x_t, J(x_t-z)\rangle \\
= -\frac{1}{t}[\|x_t-z\|^2-\langle BQ_Cx_t-BQ_Cz, J(x_t-z)\rangle]\\+\langle \sum\limits_{i = 1}^{\infty}b_i F_i(I-BQ_C)x_t, J(x_t-z)\rangle\\
\leq \langle \sum\limits_{i = 1}^{\infty}b_i F_i(I-BQ_C)x_t, J(x_t-z)\rangle.
$ |
Taking the limits on both sides of the above inequality,
| $
\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)p_0, J(p_0-z)\rangle \leq 0
$ |
since $x_n \rightarrow p_0$ and $J$ is uniformly continuous on each bounded subsets of $E.$
Thus $p_0$ satisfies the variational inequality (2.2).
Now assume there exists another subsequence $\{x_m\}$ of $\{x_t\}$
satisfying $x_m \rightarrow q_0.$ Then Step 4 implies that $BQ_Cx_m \rightarrow q_0.$ From Lemma 1.3, we know that $I-BQ_C$
is demiclosed at zero, then $q_0 = BQ_Cq_0$ which ensures that $ q_0\in {\rm{Fix}}(B).$ Repeating the above proof, we can also know that $q_0$ solves variational inequality (2.2). Thus $p_0 = q_0$ in view of Step 5.
Hence $x_t \rightarrow p_0, $ as $t \rightarrow 0, $ which is the unique solution of the variational inequality (2.2).
This completes the proof.
Theorem 2.2 Let $E, C, Q_C, f_i, F_i, k$ and $\overline{\gamma}$ be the same as those in theorem 2.1, and let $A_i: C \rightarrow C$ be
m-accretive operator, for $i\in N^+.$ Let $\{\alpha_n\}, $ $\{\delta_n\}, $ $\{\beta_n\}, $
$\{\zeta_n\}, $ $\{\gamma_n\}$, $\{a_n\}$, $\{b_n\}$ and $\{c_n\}$ be real number sequences in (0, 1) with
$\sum\limits_{i = 1}^{\infty}a_i=\sum\limits_{i = 1}^{\infty}b_i=\sum\limits_{i = 1}^{\infty}c_i = 1.$ Let
$\{r_{n, i}\}\subset (0, +\infty)$ for $i \in N^+$, $\{\varepsilon'_n\}\subset E$ and $\{\varepsilon"_n\}\subset C$. Suppose
| $
D : =
\bigcap\limits_{i = 1}^{\infty}A_i^{-1}0\neq \emptyset,\;\; \sum\limits_{i = 1}^{\infty}\|f_i\| <+\infty, \;\;\sum\limits_{i = 1}^{\infty}b_i\|F_i\| <+\infty
$ |
and $0 < \eta < \frac{\overline{\gamma}}{2k}$.
Let $\{x_n\}$ be
generated by the following iterative scheme
| $
\left\{ \begin{array}{l}
{x_0} \in E,\\
{y_n} = {Q_C}[(1 - {\alpha _n})({x_n} + {{\varepsilon '}_n})],\\
{z_n} = {\beta _n}{y_n} + {\gamma _n}\sum\limits_{i = 1}^\infty {{c_i}} J_{{r_{n,i}}}^{{A_i}}(\frac{{{y_n} + {z_n}}}{2}) + {\delta _n}\varepsilon{{\rm{"}}_n},\\
{x_{n + 1}} = {\zeta _n}\eta \sum\limits_{i = 1}^\infty {{a_i}} {f_i}({x_n}) + (I - {\zeta _n}\sum\limits_{i = 1}^\infty {{b_i}} {F_i})\sum\limits_{i = 1}^\infty {{c_i}} J_{{r_{n,i}}}^{{A_i}}{z_n},\quad n \ge 0.
\end{array} \right.
$ |
(A) |
Then $\{x_n\}$ converges
strongly to the unique element $p_0 \in D, $ which satisfies the
following variational inequality: for $\forall z \in D, $
| $
\langle (\sum\limits_{i = 1}^{\infty}b_i F_i - \eta \sum\limits_{i = 1}^{\infty}a_i f_i)p_0, J(p_0-z)\rangle \leq 0,
$ |
(2.7) |
under the assumptions that
(ⅰ) $\sum\limits_{n=0}^{\infty} \alpha_n <+\infty, $ $\sum\limits_{n=0}^{\infty} \delta_n <+\infty, $ $\sum\limits_{n=0}^{\infty}\|\varepsilon'_n\| < +\infty, $
$\sum\limits_{n=0}^{\infty}\|\varepsilon"_n\| < +\infty$;
$(ⅱ)$ $\sum\limits_{n=0}^{\infty}\zeta_n = +\infty$ and $\zeta_n \rightarrow 0$ as $n \rightarrow \infty$;
$(ⅲ)$ $\frac{\alpha_n}{\zeta_n}\rightarrow 0, $ $\frac{\delta_n}{\zeta_n}\rightarrow 0, $$\frac{\|\varepsilon'_n\|}{\zeta_n}\rightarrow 0$;
$(ⅳ)$ $\delta_n + \beta_n + \gamma_n \equiv 1, $ for $n \geq 0.$
Proof We shall split the proof into five steps.
Step 1 $\{x_n\}$ is well-defined.
In fact, it suffices to show that $\{z_n\}$ is well-defined.
For $t, s\in (0, 1)$, define $U_{t, s}: C
\rightarrow C$ by $U_{t, s} x: = tu + sB(\frac{u+x}{2})+(1-t-s)v, $
where $B: C \rightarrow C$ is nonexpansive and $x, u, v \in C$.
Then
| $
\|U_{t, s} x - U_{t, s}y\|\leq
s\|\frac{u+x}{2}-\frac{u+y}{2}\| \leq \frac{s}{2} \|x-y\|.
$ |
Thus $U_{t, s}$ is a contraction, which ensures from Lemma 1.2 that
there exists $x_{t, s}\in C$ such that $U_{t, s} x_{t, s} =
x_{t, s}.$ That is, $x_{t, s} = tu +
sB(\frac{u+x_{t, s}}{2})+(1-t-s)v$.
Since $J_{r_{n, i}}^{A_i}$ is nonexpansive and $\sum\limits_{i =
1}^{\infty}c_i = 1$, then $\sum\limits_{i =
1}^{\infty}c_iJ_{r_{n, i}}^{A_i}$ is nonexpansive, which implies that $\{z_n\}$ is well-defined, and then $\{x_n\}$
is well-defined.
Step 2 $\{x_n\}, $ $\{y_n\}$ and $\{z_n\}$ are all bounded.
$\forall p \in D, $ we see that for $n \geq 0, $
| $
\|y_{n} - p\|\leq (1-\alpha_n)\|x_n-p\|+(1-\alpha_n)\|\varepsilon'_n\|+\alpha_n \|p\|.
$ |
(2.8) |
Therefore, for $p \in D$ and $n \geq 0, $ we have
| $
\|z_{n} - p\|\leq \beta_{n}\|y_n-p\|+\gamma_n\|\sum\limits_{i = 1}^{\infty}
c_i J_{r_{n, i}}^{A_i}(\frac{y_n+z_n}{2})-p\|+\delta_n\|\varepsilon"_n-p\|\\
\;\;\;\;\;\;\;\;\;\;\;\;\leq
(\beta_n+\frac{\gamma_{n}}{2})\|y_n-p\|+\frac{\gamma_n}{2}\|z_n-p\|+\delta_n\|\varepsilon"_n-p\|\\\;\;\;\;\;\;\;\;\;\;\;\;
\leq
(1-\frac{\gamma_{n}}{2})\|y_n-p\|+\frac{\gamma_n}{2}\|z_n-p\|+\delta_n\|\varepsilon"_n-p\|,
$ |
which implies that
| $
\|z_n - p\| \leq
\|y_n-p\|+\frac{2\delta_n}{2-\gamma_n}\|\varepsilon"_n-p\|\leq \|y_n - p\|
+2\|\varepsilon"_n\|+\frac{2\delta_n}{2-\gamma_n}\|p\|.
$ |
(2.9) |
Using Lemma 1.1, (2.8) and (2.9), we have: for $n \geq 0, $
| $
\|x_{n+1} - p\| \\
\leq \zeta_n \eta \sum\limits_{i=1}^{\infty}a_i\|f_i(x_n)-f_i(p)\|+ \zeta_n \|\eta\sum\limits_{i=1}^{\infty}a_if_i(p)-\sum\limits_{i=1}^{\infty}b_iF_i(p)\|\\
+\|I-\zeta_n\sum\limits_{i=1}^{\infty}b_iF_i\|\|z_n - p\|\\
\leq \zeta_n \eta k\|x_n-p\|+ \zeta_n\|\eta\sum\limits_{i=1}^{\infty}a_if_i(p)-\sum\limits_{i=1}^{\infty}b_iF_i(p)\|
+(1-\zeta_n \overline{\gamma})\|z_n - p\|\\
\leq [1-\zeta_n(\overline{\gamma}-k \eta)]\|x_n-p\|+ \zeta_n \|\eta\sum\limits_{i=1}^{\infty}a_if_i(p)-\sum\limits_{i=1}^{\infty}b_iF_i(p)\|\\
+\|\varepsilon'_n\|+2\|\varepsilon"_n\|+\|p\|(\alpha_n+\frac{2\delta_n}{2-\gamma_n}).\\
$ |
(2.10) |
By using the inductive method, we can easily get the following
result from (2.10)
| $\|x_{n+1}-p\|
\leq {\rm{max}}\{\|x_0 - p\|, \frac{\|\eta\sum\limits_{i=1}^{\infty}a_if_i(p)
-\sum\limits_{i=1}^{\infty}b_iF_i(p)\|}{\overline{\gamma}-k \eta}\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+ \sum\limits_{k=0}^{n}\|\varepsilon'_k\|+2
\sum\limits_{k=0}^{n}\|\varepsilon"_k\|+\|p\|(\sum\limits_{k=0}^{n}\alpha_k+\sum\limits_{k=0}^{n}\frac{2\delta_k}{2-\gamma_k}).
$ |
Therefore, from assumptions $(i)$, we know that
$\{x_n\}$ is bounded. Set $M = {\rm{sup}}\{ \|x_n\|, \|\varepsilon'_n\| : n \geq 0\}.$ Then $M$ is a
positive constant.
Step 3 ${\rm{Fix}}(\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i})= D.$
It is obvious that $A_i^{-1}0 = {\rm{Fix}}(J_{r_{n, i}}^{A_i})$ for $i \in N^+$. Lemma 1.4 implies that $\bigcap\limits_{i=1}^{\infty}{\rm{Fix}}(J_{r_{n, i}}^{A_i})= {\rm{Fix}}(\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}).$ Thus ${\rm{Fix}}(\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i})= D.$
Step 4
| $
\|x_{n+1} - p_0\|^2 \leq (1-\omega_n^{(1)})\|x_{n} - p_0\|^2 + \omega_n^{(1)}\omega_n^{(2)}-\omega_n^{(3)},
$ |
(2.11) |
where $p_0$ is the unique solution of variational inequality (2.7), $ M' = 4M+2\|p_0\|$,
| $
\omega_n^{(1)}= \frac{\zeta_n (\overline{\gamma}-2\eta k)}{1-\zeta_n\eta k},
$ |
| $
\omega_n^{(2)}= \frac{1}{\zeta_n (\overline{\gamma}-2\eta k)}(\|\varepsilon_n'\|M'+\alpha_n M'\|p_0\|+\frac{2\delta_n}{2-\gamma_n}\|\varepsilon"_n - p_0\|^2)\\\;\;\;\;\;\;\;\;\;\;\;+ \frac{2\langle \eta \sum\limits_{i=1}^{\infty}a_if_i(p_0)-\sum\limits_{i=1}^{\infty}b_i F_i(p_0), J(x_{n+1}-p_0)\rangle} {\overline{\gamma}-2 \eta k},
$ |
| $
\omega_n^{(3)} = \frac{(1-\zeta_n \overline{\gamma})^2}{1-\zeta_n \eta k}\frac{2\gamma_n}{2-\gamma_n}\sum\limits_{i=1}^{\infty}c_i \varphi(\|\frac{y_n+z_n}{2}-J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|).
$ |
Since $\sum\limits_{i =
1}^{\infty} c_i J_{r_{n, i}}^{A_i}: C \rightarrow C$ is nonexpansive, then using Theorem 2.1, we know that there
exists $z_t$ such that
| $
z_t = t\eta \sum\limits_{i=1}^{\infty}a_if_i(z_t)+(I-\sum\limits_{i=1}^{\infty}b_iF_i)\sum\limits_{i=1}^{\infty}c_iJ^{A_i}_{r_{n, i}}Q_Cz_t
$ |
(2.12) |
for $t \in
(0, (\sum\limits_{i=1}^{\infty}b_i\|F_i\|)^{-1}).$ Moreover, $z_t \rightarrow p_0 \in D, $ as $t \rightarrow
0, $ which is the unique solution of the variational
inequality (2.7).
For this $p_0 \in D, $ using Lemma 1.5, we have
| $
\|y_n - p_0\|^2 \leq \|(1-\alpha_n)(x_n+\varepsilon_n') - p_0\|^2\\
\leq (1-\alpha_n)^2 \|x_n - p_0\|^2 + 2\langle (1-\alpha_n) \varepsilon_n' - \alpha_np_0, J[(1-\alpha_n)(x_n+\varepsilon_n')-p_0]\rangle\\
\leq (1-\alpha_n)^2 \|x_n - p_0\|^2 + \|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'.
$ |
(2.13) |
And, using Lemma 1.6,
| $\|z_n - p_0\|^2\leq \beta_n \|y_n - p_0\|^2\\+ \gamma_n\sum\limits_{i=1}^{\infty}c_i\|J_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})-p_0\|^2 + \delta_n \|\varepsilon_n"-p_0\|^2\\
\leq \beta_n \|y_n - p_0\|^2+ \gamma_n\sum\limits_{i=1}^{\infty}c_i[\|\frac{y_{n}+z_n}{2}-p_0\|^2\\-\varphi(\|(I-J^{A_i}_{r_{n, i}})(\frac{y_n+z_n}{2})\|)] + \delta_n \|\varepsilon_n"-p_0\|^2\\
\leq (\beta_n + \frac{\gamma_n}{2})\|y_n - p_0\|^2+ \delta_n \|\varepsilon_n"-p_0\|^2\\-\gamma_n \sum\limits_{i=1}^{\infty}c_i\varphi(\|(I- J^{A_i}_{r_{n, i}})(\frac{y_n+z_n}{2})\|)+ \frac{\gamma_n}{2}\|z_n - p_0\|^2,
$ |
which implies that
| $
\|z_n - p_0\|^2\leq \frac{2\beta_n + \gamma_n}{2-\gamma_n}\|y_n - p_0\|^2\\\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{2\delta_n}{2-\gamma_n} \|\varepsilon_n"-p_0\|^2-\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|)\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\; \leq (1-\alpha_n)^2 \|x_n - p_0\|^2 + \|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'+ \frac{2\delta_n}{2-\gamma_n} \|\varepsilon_n"-p_0\|^2\\
\;\;\;\;\;\;\;\;\;\;\; \;\;\; -\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|).
$ |
(2.14) |
Now, noticing Step 1 in Theorem 2.1 and using Lemma 1.5 again,
| $
\|x_{n+1} - p_0\|^2 \\= \|(I - \zeta_n \sum\limits_{i=1}^{\infty}b_iF_i)\sum\limits_{i=1}^{\infty}c_iJ^{A_i}_{r_{n, i}}(z_n - p_0)+ \zeta_n(\eta \sum\limits_{i=1}^{\infty}a_if_i(x_n) -\sum\limits_{i=1}^{\infty}b_i F_ip_0)\|^2\\
\leq (1-\zeta_n \overline{\gamma})^2\|z_n - p_0\|^2+ 2\zeta_n\langle \eta \sum\limits_{i=1}^{\infty}a_if_i(x_n) -\sum\limits_{i=1}^{\infty}b_i F_ip_0, J(x_{n+1}-p_0)\rangle\\
\leq (1-\zeta_n \overline{\gamma})\|x_n - p_0\|^2+ \|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'\\- (1-\zeta_n \overline{\gamma})^2\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|)\\+ \frac{2\delta_n}{2-\gamma_n} \|\varepsilon_n"-p_0\|^2 + 2\zeta_n\langle \eta \sum\limits_{i=1}^{\infty}a_i(f_i(x_n) -f_i(p_0)), J(x_{n+1}-p_0)\rangle\\
+ 2\zeta_n \langle \eta\sum\limits_{i=1}^{\infty}a_if_i(p_0)-\sum\limits_{i=1}^{\infty}b_i F_ip_0, J(x_{n+1}-p_0)\rangle \\
\leq (1-\zeta_n \overline{\gamma})\|x_n - p_0\|^2+ \|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'\\- (1-\zeta_n \overline{\gamma})^2\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|)\\+ \frac{2\delta_n}{2-\gamma_n} \|\varepsilon_n"-p_0\|^2 + 2\zeta_n\eta k\|x_{n}-p_0\|\|x_{n+1}-p_0\|\\+ 2\zeta_n \langle \eta\sum\limits_{i=1}^{\infty}a_if_i(p_0)-\sum\limits_{i=1}^{\infty}b_i F_ip_0, J(x_{n+1}-p_0)\rangle \\
\leq (1-\zeta_n \overline{\gamma})\|x_n - p_0\|^2+ \|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'\\- (1-\zeta_n \overline{\gamma})^2\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|)\\+ \frac{2\delta_n}{2-\gamma_n} \|\varepsilon_n"-p_0\|^2 +\zeta_n\eta k(\|x_{n}-p_0\|^2 + \|x_{n+1}-p_0\|^2)\\+ 2\zeta_n \langle \eta\sum\limits_{i=1}^{\infty}a_if_i(p_0)-\sum\limits_{i=1}^{\infty}b_i F_ip_0, J(x_{n+1}-p_0)\rangle. \\
$ |
Thus
| $
\|x_{n+1} - p_0\|^2\\\leq \frac{1-\zeta_n\overline{\gamma}+\zeta_n \eta k}{1-\zeta_n\eta k}\|x_n - p_0\|^2 + \frac{1}{1-\zeta_n\eta k} [\|\varepsilon_n'\|M'+\alpha_n \|p_0\|M'+\frac{2\delta_n}{2-\gamma_n}\|\varepsilon_n"-p_0\|^2]\\
+\frac{2\zeta_n}{1-\zeta_n \eta k}\langle \sum\limits_{i=1}^{\infty}a_if_i(p_0) - \sum\limits_{i=1}^{\infty}b_i F_ip_0, J(x_{n+1}-p_0)\rangle \\- \frac{(1-\zeta_n\overline{\gamma})^2}{1-\zeta_n \eta k}\frac{2\gamma_n}{2-\gamma_n} \sum\limits_{i=1}^{\infty}c_i\varphi(\|\frac{y_n+z_n}{2}- J^{A_i}_{r_{n, i}}(\frac{y_n+z_n}{2})\|)\\
= (1-\omega_n^{(1)})\|x_{n} - p_0\|^2 + \omega_n^{(1)}\omega_n^{(2)}-\omega_n^{(3)}.\\
$ |
It follows from the assumption(ⅱ) that
$\omega_n^{(1)}\rightarrow 0, $ as $n \rightarrow +\infty$.
Step 5 $x_n \rightarrow p_0, $ as $n \rightarrow +\infty$, where $p_0$ is the same as that in Step 4.
Our next discussion will be divided into two cases:
Case 1. $\{\|x_n - p_0\|\}$ is decreasing.
If $\{\|x_n - p_0\|\}$ is decreasing, we know from the result of Step 4 that
| $
0 \leq \omega_n^{(3)}\leq \omega_n^{(1)}(\omega_n^{(2)}-\|x_n - p_0\|^2)+(\|x_n - p_0\|^2-\|x_{n+1} - p_0\|^2)\rightarrow 0,
$ |
which ensures that
| $
\sum\limits_{i=1}^{\infty}c_i \varphi(\|\frac{y_n+z_n}{2}-J_{r_{n, i}}^{A_i}( \frac{y_n+z_n}{2})\|)\rightarrow 0,
$ |
as $n \rightarrow +\infty$. Then
from the property of $\varphi$, we know that
| $
\sum\limits_{i=1}^{\infty}c_i \|\frac{y_n+z_n}{2}-J_{r_{n, i}}^{A_i}( \frac{y_n+z_n}{2})\|\rightarrow 0,
$ |
as $n \rightarrow +\infty$. Since
| $
\|y_n - z_n\|\leq \gamma_n \sum\limits_{i=1}^{\infty}c_i\|J_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})-y_n\| + \delta_n \|\varepsilon"_n - y_n\|\\
\leq \gamma_n \sum\limits_{i=1}^{\infty}c_i\|J_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})-\frac{y_{n}+z_n}{2}\| +\gamma_n \|\frac{y_{n}+z_n}{2}-y_n\|+ \delta_n \|\varepsilon"_n - y_n\|,
$ |
then
| $
\|y_n - z_n\|\leq \frac{2}{2-\gamma_n}[\gamma_n \sum\limits_{i=1}^{\infty}c_i\|J_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})-\frac{y_n+z_n}{2}\| + \delta_n \|\varepsilon"_n-y_n\|]
\rightarrow 0,
$ |
as $n \rightarrow +\infty$. Therefore,
| $
\|y_n - \sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}y_n\|\\
\leq \|y_n - z_n\|+\|z_n - \sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})\| \\+ \|\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})-\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}y_n\|\\
\leq \frac{3}{2}\|y_n - z_n\|+\beta_n\|y_n - \sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})\| \\+ \delta_n \|\varepsilon"_n-\sum\limits_{i=1}^{\infty}c_iJ_{r_{n, i}}^{A_i}(\frac{y_{n}+z_n}{2})\|\rightarrow 0.\\
$ |
Next, we shall show that
| $
{\rm{lim}}\;\mathop {{\rm{sup}}}\limits_{n \to + \infty } \langle \eta \sum\limits_{i = 1}^\infty {{a_i}} {f_i}({p_0}) - \sum\limits_{i = 1}^\infty {{b_i}} {F_i}({p_0}),J({x_{n + 1}} - {p_0})\rangle \le 0.
$ |
(2.15) |
Let $z_t$ be the same as that in (2.12). Since $\|z_t\|\leq \|z_t - p_0 \|+\|p_0\|, $ then $\{z_t\}$ is
bounded, as $t \rightarrow 0$. Using Lemma 1.5, we have
| $
\|z_t - y_{n}\|^2 = \|z_t - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n+\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n - y_n\|^2\\
\leq \|z_t - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n\|^2 + 2\langle \sum\limits_{i =
1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n - y_n, J(z_t - y_n) \rangle \\
= \|t\eta \sum\limits_{i = 1}^{\infty} a_if_i(z_t) + (I-t\sum\limits_{i = 1}^{\infty} b_iF_i)\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_{n}\|^2\\+ 2\langle \sum\limits_{i =
1}^{\infty}c_i
J_{r_{n, i}}^{A_i}y_n - y_n, J(z_t - y_n) \rangle \\
\leq \|\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_{n}\|^2 \\+ 2t\langle \eta \sum\limits_{i = 1}^{\infty} a_i
f_i(z_t) - \sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t), J(z_t - \sum\limits_{i =
1}^{\infty} c_i J_{r_{n, i}}^{A_i}y_n) \rangle \\+2\langle \sum\limits_{i =
1}^{\infty}c_i
J_{r_{n, i}}^{A_i}y_n - y_n, J(z_t - y_n) \rangle\\
\leq \|z_t - y_{n}\|^2 + 2t\langle \eta \sum\limits_{i = 1}^{\infty} a_i
f_i(z_t) - \sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t), J(z_t - \sum\limits_{i =
1}^{\infty} c_i J_{r_{n, i}}^{A_i}y_n) \rangle \\ + 2 \| \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n - y_n\|\|z_t - y_n\|
,
$ |
which implies that
| $
t\langle \sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(z_t), J(z_t - \sum\limits_{i
= 1}^{\infty} c_i J_{r_{n, i}}^{A_i}y_n) \rangle
\\ \leq \| \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n - y_n\|\|z_t-y_{n}\|.
$ |
So
| $
\mathop {{\rm{lim}}}\limits_{t \to 0} \;\mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to + \infty } \langle \sum\limits_{i = 1}^\infty {{b_i}} {F_i}(\sum\limits_{i = 1}^\infty {{c_i}} J_{{r_{n,i}}}^{{A_i}}{Q_C}{z_t}) - \eta \sum\limits_{i = 1}^\infty {{a_i}} {f_i}({z_t}),J({z_t} - \sum\limits_{i = 1}^\infty {{c_i}} J_{{r_{n,i}}}^{{A_i}}{y_n})\rangle \le 0.
$ |
Since $z_t \rightarrow p_0, $ then
| $
\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t \rightarrow \sum\limits_{i =
1}^{\infty} c_i J_{r_{n, i}}^{A_i}Q_Cp_0 = p_0
$ |
as $t \rightarrow 0$. Noticing that
| $
\langle \sum\limits_{i = 1}^{\infty} b_iF_i(p_0)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(p_0), J(p_0 - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n)\rangle \\
=\langle\sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cp_0)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(p_0), J(p_0 - \sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}y_n)- J(z_t -\sum\limits_{i = 1}^{\infty}
c_i J_{r_{n, i}}^{A_i}y_n)\rangle\\
+ \langle\sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cp_0)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(p_0)-\sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t)\\+\eta \sum\limits_{i = 1}^{\infty} a_i f_i(z_t), J(z_t -\sum\limits_{i = 1}^{\infty}
c_i J_{r_{n, i}}^{A_i}y_n)\rangle \\
+ \langle \sum\limits_{i = 1}^{\infty} b_iF_i(\sum\limits_{i = 1}^{\infty} c_i
J_{r_{n, i}}^{A_i}Q_Cz_t)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(z_t), J(z_t -\sum\limits_{i
= 1}^{\infty} c_i J_{r_{n, i}}^{A_i}y_n)\rangle,
$ |
then we have
| $
\mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to + \infty } \langle \sum\limits_{i = 1}^{\infty} b_iF_i(p_0)-\eta \sum\limits_{i = 1}^{\infty} a_if_i(p_0), J(p_0-\sum\limits_{i = 1}^{\infty} c_iJ_{r_{n, i}}^{A_i}y_n)\rangle\leq 0.
$ |
Since $y_n - z_n \rightarrow 0, $ then $x_{n+1}-\sum\limits_{i = 1}^{\infty} c_i J_{r_{n, i}}^{A_i}y_n \rightarrow 0, $ which implies that
| $
\mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to + \infty } \langle \sum\limits_{i = 1}^{\infty} b_iF_i(p_0)-\eta \sum\limits_{i = 1}^{\infty} a_i f_i(p_0), J(p_0 - x_{n+1})\rangle \leq 0.
$ |
Assumption (ii) and (2.15) ensure that $\mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to + \infty }\omega_n^{(2)}\leq 0.$
Employing (2.11) again, we have
| $
\|x_n - p_0\|^2 \leq \frac{\|x_n - p_0\|^2 - \|x_{n+1} - p_0\|^2 }{\omega_n^{(1)}}+\omega_n^{(2)}.
$ |
Assumption (ⅱ) implies that $lim_{n \rightarrow \infty}\frac{\|x_n - p_0\|^2 - \|x_{n+1} - p_0\|^2 }{\omega_n^{(1)}} = 0.$ Then
| $
\mathop {{\rm{lim}}}\limits_{n \to \infty } {\left\| {{x_n} - {p_0}} \right\|^2} \le \mathop {{\rm{lim}}\;{\rm{inf}}}\limits_{n \to \infty } \frac{{{{\left\| {{x_n} - {p_0}} \right\|}^2} - {{\left\| {{x_{n + 1}} - {p_0}} \right\|}^2}}}{{\omega _n^{(1)}}} + \mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to \infty } \omega _n^{(2)} \le 0.
$ |
Then the result that $x_n \rightarrow p_0$ follows.
Case 2 If $\{\|x_n - p_0\|\}$ is not eventually decreasing, then we can find a subsequence $\{\|x_{n_m} - p_0\|\}$ so that $\|x_{n_m} - p_0\|\leq \|x_{n_{m+1}} - p_0\|$ for all $m \geq 1.$ From Lemma 1.7, we can define a subsequence $\{\|x_{\tau(n)} - p_0\|\}$ so that $\max\{\|x_{\tau(n)} - p_0\|, \|x_n - p_0\|\}\leq \|x_{\tau(n)+1} - p_0\|$ for all $n > n_1.$ This enable us to deduce that (similar to Case 1)
| $
0 \leq \omega_{\tau(n)}^{(3)}\leq \omega_{\tau(n)}^{(1)}(\omega_{\tau(n)}^{(2)}-\|x_{\tau(n)} - p_0\|^2)+(\|x_{\tau(n)} - p_0\|^2-\|x_{{\tau(n)}+1} - p_0\|^2)\rightarrow 0,
$ |
and then copy Case 1, we have $\mathop {{\rm{lim}}}\limits_{n \to \infty } \|x_{\tau(n)} - p_0\| = 0.$ Thus $ 0 \leq \|x_{n} - p_0\|\leq \|x_{\tau(n)+1} - p_0\|\rightarrow 0, $ as $n \rightarrow \infty.$ This completes the proof.
Remark 2.1 In similar studies, e.g. [5], they usually have the following strong restrictions on the parameters: $\sum\limits_{i = 1}^{\infty}|r_{n+1, i} - r_{n, i}| <+\infty, $ $r_{n, i}\geq \varepsilon > 0, 0 < \mathop {{\rm{lim}}\;{\rm{inf}}}\limits_{n \to \infty } \gamma_n \leq \mathop {{\rm{lim}}\;{\rm{sup}}}\limits_{n \to \infty } \gamma_n < 1$ and $\gamma_{n+1}-\gamma_n \rightarrow 0.$ By using new tools of Lemmas 1.6 and 1.7, these strong restrictions are deleted in our paper.
Remark 2.2 In scheme (A), let $E = C = (-\infty, +\infty), a_i = c_i = \frac{1}{2^i}, b_i = \frac{7}{8^i}, $ $f_i(x) = \frac{x}{2^i}, k = \frac{1}{2}, $
$F_i x = \frac{4^i}{7}x, \overline{\gamma} = \frac{4}{7}, \eta = \frac{1}{7}, \alpha_n = \beta_n = \delta_n = \varepsilon_n' = \varepsilon_n" = \frac{1}{(n+1)^2}, \zeta_n = \frac{1}{n+1}, r_{n, i} = (n+1)2^i$ and $A_i x = \frac{x}{2^i}$ for $i \in N^+$ and $n \geq 0.$ Then all of the assumptions in Theorem 2.2 are satisfied and $D = \{0\}.$ By using Visual Basic six, we get Table 2.1 and Figure 2.1 below, from which we can see the convergence of $\{x_n\}$.
表 2.1
(Table 2.1)
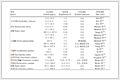
Table 2.1 Numerical Results of $\{x_n\}$ with Initial $x_0 = -8.0$
| n |
yn |
zn |
xn |
| 0 |
0.000000 |
0.8000000 |
-8.000000 |
| 1 |
-0.0982143 |
0.0324675 |
-0.3809524 |
| 2 |
0.0955130 |
0.0357167 |
-0.00365904 |
| 3 |
0.0641200 |
0.0148211 |
0.00589470 |
| 4 |
0.0406016 |
0.0068630 |
0.00229334 |
| 5 |
0.0279171 |
0.0036785 |
0.00093691 |
| 6 |
0.0204279 |
0.0021893 |
0.00044536 |
| 7 |
0.0156147 |
0.0014041 |
0.00023759 |
| 8 |
0.0123295 |
0.0009523 |
0.00013792 |
| 9 |
0.0099845 |
0.0006747 |
0.00008538 |
| 10 |
0.0082513 |
0.0004949 |
0.00005561 |
| 11 |
0.0069337 |
0.0003735 |
0.00003773 |
| 12 |
0.0059085 |
0.0002887 |
0.00002649 |
|
Table 2.1
Numerical Results of $\{x_n\}$ with Initial $x_0 = -8.0$
|
 2018, Vol. 38
2018, Vol. 38  Issue (2): 269-284
Issue (2): 269-284 2018, Vol. 38
2018, Vol. 38  Issue (2): 269-284
Issue (2): 269-284