Gorenstein homological theory originated from the works of Auslander and Bridger [1], where they introduced modules of $G$-dimension $0$. Enochs et al. [2, 3] extended these ideas and introduced Gorenstein projective, Gorenstein injective and Gorenstein flat modules and corresponding dimensions over arbitrary rings. From then, Gorenstein homological theory was extensively studied and developed, see for example, [4, 5] and references therein.

Recall from White [6] that an $R$-module $C$ is said to be semidualizing if $C$ admits a degreewise finite projective resolution, the natural homothety map $R \rightarrow {\rm {Hom}}_{R}(C, C)$ is an isomorphism and $\rm{Ext}^{\geq1}_{R}(C, C)=0.$ Examples include the rank one free modules and a dualizing (Canonical) modules when one exists. With this notion, Gorenstein homological theory with respect to a semidualizing module was extensively studied, see for example, [7] and [8].

Let $R$ be a ring. White [6] initiated the study of $G_{C}$-projective $R$-modules as the modules of the form ${\rm {Im}}$$(P_{0}\rightarrow C\otimes_{R}P^{0})$ for some exact sequence of $R$-modules

$ {\bf{P}}: \cdots \rightarrow P_{1} \rightarrow P_{0} \rightarrow C\otimes_{R}P^{0} \rightarrow C\otimes_{R}P^{1} \rightarrow \cdots, $

where each $P_{i}$ and $P^{i}$ is projective, and such that the complex ${\rm {Hom}}_{R}({\bf{P}}, C\otimes_{R}Q)$ is exact for each projective $R$-module $Q$. The complex ${\bf{P}}$ is called a complete $PC$-resolution. When $C=R$, the definition corresponds to the definition of Gorenstein projective modules. In [6], Proposition 2.6 showed that if $P$ is $R$-projective, then $P$ and $C\otimes_{R}P$ are $G_{C}$-projective, and Proposition 2.9 showed that every cokernel in a complete $PC$-resolution is $G_{C}$-projective, so every image and kernel in it is also $G_{C}$-projective.

For $G_{C}$-projective $R$-modules, we give another generalization in this paper, which is different from the definition above and that in [9]. An $R$-module $M$ is called Gorenstein $C$-projective if there exists an exact sequence of $R$-modules

$ {\bf{X}}: \cdots \rightarrow C\otimes_{R}P_{1} \rightarrow C\otimes_{R}P_{0} \rightarrow C\otimes_{R}P^{0} \rightarrow C\otimes_{R}P^{1} \rightarrow \cdots, $

where each $P_{i}$ and $P^{i}$ is projective with $M\cong$ ${\rm {Im}}$$(C\otimes_{R}P_{0}\rightarrow C\otimes_{R}P^{0}), $ such that the complex ${\rm {Hom}}_{R}({\bf{X}}, C\otimes_{R}Q)$ is exact for each projective $R$-module $Q$. It is easy to see that, for every projective $R$-module $P$, $C\otimes_{R}P$ is Gorenstein $C$-projective from definition, while the projective module $P$ is not Gorenstein $C$-projective, so Gorenstein $C$-projective modules are a generalization of $P_{C}$-projective modules not projective modules, which distinguishes $G_{C}$-projective modules. When $C=R$, Gorenstein $C$-projective modules are exactly Gorenstein projective modules. From this point of view, the notion of Gorenstein $C$-projective modules is a generalization of Gorenstein projective modules.

Let $\mathscr{A}$ be an abelian category and $\mathcal{X}$ an additive full-subcategory of $\mathscr{A}.$ Sather-Wagstaff, Sharif and White [9] introduced the definition of Gorenstein category $\mathcal {G}(\mathcal{X})$ on $\mathcal{X}$. $\mathcal {G}(\mathcal{X})=\{A\in\mathscr{A}\mid$ there exists a both ${{\rm{Hom}}}_{\mathscr{A}}(\mathbb{X}, -)$-exact and ${\rm {Hom}}_{\mathscr{A}}(-, \mathbb{X})$-exact exact sequence $\mathbb{X}:\cdots\rightarrow X_{1}\rightarrow X_{0}\rightarrow X^{0}\rightarrow X^{1}\rightarrow \cdots$ in $\mathscr{A}$ with all $X_{i}$ and $ X^{i}$ in $\mathcal{X}$ and $A\cong{\rm{Im}}$$(X_{0}\rightarrow X^{0})$$\}$. Especially, if $\mathscr{A}=$ $R$-Mod, $\mathcal {X}=\mathcal{P}(R), $ then $\mathcal {G}(\mathcal {P}(R))$ is nothing but the subcategory of Gorenstein projective modules. Dually, $\mathcal {G}(\mathcal {I}(R))$ is nothing but the subcategory of Gorenstein injective modules. Let $\mathcal{G}^{0}(\mathcal {X})=\mathcal {X}, $ $\mathcal {G}^{1}(\mathcal{X})=\mathcal {G}(\mathcal {X})$, for arbitrary $n\geq1$, $\mathcal{G}^{n+1}(\mathcal {X})=\mathcal {G}^{n}(\mathcal {G}(\mathcal{X})).$ They proved that when $\mathcal{X}$ is self-orthogonal, $\mathcal {G}^{n}(\mathcal {X})=\mathcal{G}(\mathcal {X})$ for arbitrary $n\geq1$; and they proposed the question whether $\mathcal{G}^{n}(\mathcal{X})=\mathcal{G}(\mathcal{X})$ holds for an arbitrary subcategory $\mathcal{X}$. See [9, 4.10 and 5.8]. Huang [10] proved that the answer to this question is affirmative. Kong and Zhang [11] gave a slight generalization of this stability by a different method. Recently, stability of other Gorenstein classes of modules was extensively studied by many authors, see for example, [12-15]. Inspired by these results, we consider the following questions:

Question 1 Given an exact sequence of Gorenstein $C$-projective $R$-modules ${\bf{G}}:\cdots\rightarrow G_{1}\rightarrow G_{0}\rightarrow G^{0}\rightarrow G^{1}\rightarrow \cdots$ such that the complex ${{\rm{Hom}}}_{R}({\bf{G}}, {\rm C}\otimes_{R}P~)$ is exact for each $P\in \mathcal {P}(R), $ is the module ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$ Gorenstein $C$-projective?

The same question of Gorenstein $C$-injective $R$-modules can be considered dually.

Question 2 Given an exact sequence of Gorenstein $C$-flat $R$-modules ${\bf{G}}:\cdots\rightarrow G_{1}\rightarrow G_{0}\rightarrow G^{0}\rightarrow G^{1}\rightarrow \cdots$ such that the complex ${{\rm{Hom}}}_{R}(C, E)\otimes_{R}{\bf{G}}$ is exact for each $E\in \mathcal {I}(R)$, is the module ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$ Gorenstein $C$-flat?

In this paper, we give an affirmative answer to Question $1$ (see Theorem $3.5$ and Theorem $3.9$), and a partial positive answer to Question $2$ (see Theorem $3.12$). It is shown that Gorenstein $C$-projective (injective, flat) modules have a nice stability.

Throughout this paper, $R$ is a commutative ring with identity and all modules are unitary. $R$-Mod denotes the category of $R$-modules. $\mathcal{P}(R)$ (resp., $\mathcal{I}(R)$, $\mathcal{F}(R)$) denotes projective (resp., injective, flat) $R$-modules.

In this section, we mainly recall some necessary notions and definitions.

Definition 2.1 [14] Let $\mathscr{X}$, $\mathscr{Y}$ be the class of $R$-modules, $M$ be an $R$-module.

(1) An $\mathscr{X}$-resolution of $R$-module $M$ is an exact sequence

$ {\bf{X}}: \cdots\longrightarrow X_{1}\longrightarrow X_{0}\longrightarrow M\longrightarrow 0 $

with $X_{i}\in \mathscr{X}$ $(i\geq 0)$.

(2) A $\mathscr{Y}$-coresolution of $R$-module $M$ is an exact sequence

$ {\bf{Y}}: 0\longrightarrow M\longrightarrow Y_{0}\longrightarrow Y_{1}\longrightarrow \cdots $

with $Y_{i}\in \mathscr{Y}$ $(i\geq 0)$.

Definition 2.2 [5] Let $\mathcal{X}$ be a class of $R$-modules.

(1) $\mathcal{X}$ is called $\mathcal {P}_{C}(R)$-resolving if $\mathcal {P}_{C}(R)\subseteq \mathcal{X}$, and for every short exact sequence $ 0\rightarrow X'\rightarrow X\rightarrow X''\rightarrow 0$ with $X''\in \mathcal{X}$ the conditions $X'\in \mathcal{X}$ and $X\in \mathcal{X}$ are equivalent.

(2) $\mathcal{X}$ is called $\mathcal {I}_{C}(R)$-resolving if $\mathcal {I}_{C}(R)\subseteq \mathcal{X}$, and for every short exact sequence $ 0\rightarrow X'\rightarrow X\rightarrow X''\rightarrow 0$ with $X'\in \mathcal{X}$ the conditions $X\in \mathcal{X}$ and $X''\in \mathcal{X}$ are equivalent.

Recall from [6] that a module $C$ is semidualizing if $C$ admits a degreewise finite projective resolution, the natural homothety map $R \rightarrow {\rm {Hom}}_{R}(C, C)$ is an isomorphism and $\rm{Ext}^{\geq1}_{R}(C, C)=0.$ The rank one free modules and a dualizing module are semidualizing modules over a noetherian ring $R$. We refer the reader to [16-19].

In the remainder of the paper, let $C$ be a fixed semidualizing $R$-module.

Recall from [18] that the $R$-modules in the following classes

$ \begin{eqnarray*} &&\mathcal{P}_{C}(R)=\{C\otimes_{R}P\mid P \;\;\text{is a projective}\; R-{\rm module}\}, \\ &&\mathcal{F}_{C}(R)=\{C\otimes_{R}F\mid F\;\; \text{is a flat }\; R-{\rm module}\}, \\ &&7\mathcal{I}_{C}(R)=\{{\rm Hom}_{R}(C, I)\mid I \;\;\text{is an injective }\; R-{\rm module}\} \end{eqnarray*} $

are called $C$-projective, $C$-flat, and $C$-injective, respectively.

Definition 2.3  An $R$-module $M$ is said to be Gorenstein $C$-projective, if there exists an exact sequence of $C$-projective $R$-modules

$ {\bf{X}}: \cdots \rightarrow C\otimes_{R}P_{1} \rightarrow C\otimes_{R}P_{0} \rightarrow C\otimes_{R}P^{0} \rightarrow C\otimes_{R}P^{1} \rightarrow \cdots $

with $M\cong$ ${\rm {Im}}$$(C\otimes_{R}P_{0}\rightarrow C\otimes_{R}P^{0})$, such that the complex ${\rm {Hom}}_{R}({\bf{X}}, C\otimes_{R}Q)$ is exact for each projective $R$-module $Q$. The complex ${\bf{X}}$ is called complete $\mathcal{P}_{C}$-resolution, then by symmetry, all the images, and hence also all the kernels, and cokernels of ${\bf{X}}$ are Gorenstein $C$-projective modules.

Dually, Gorenstein $C$-injective modules are defined.

An $R$-module $L$ is said to be Gorenstein $C$-flat, if there exists an exact sequence of $C$-flat modules

$ {\bf{X}}: \cdots \rightarrow C\otimes_{R}F_{1} \rightarrow C\otimes_{R}F_{0} \rightarrow C\otimes_{R}F^{0} \rightarrow C\otimes_{R}F^{1} \rightarrow \cdots $

with $L\cong$ ${\rm {Im}}$$(C\otimes_{R}F_{0}\rightarrow C\otimes_{R}F^{0})$ such that the complex ${\rm {Hom}}_{R}(C, I)\otimes_{R}{\bf{X}}$ is exact for each injective $R$-module $I$.

We use the symbol $\mathcal {G}\mathcal {P}_{C}(R)$ (resp., $\mathcal{G}\mathcal {I}_{C}(R), $ $\mathcal {G}\mathcal {F}_{C}(R)$) to stand for the class of Gorenstein $C$-projective (resp., Gorenstein $C$-injective, Gorenstein $C$-flat) $R$-modules. It is obvious that $\mathcal {P}_{C}(R)\subseteq\mathcal {G}\mathcal {P}_{C}(R)$, $\mathcal {I}_{C}(R)\subseteq\mathcal {G}\mathcal {I}_{C}(R)$, $\mathcal {F}_{C}(R)\subseteq\mathcal {G}\mathcal {F}_{C}(R).$

We begin with the following:

Lemma 3.1  If $\{{\bf{X}}_{\lambda}\}_{\lambda\in\Lambda}$ is a collection of complete $\mathcal{P}_{C}$-resolution, then $\amalg_{\Lambda}{\bf{X}}_{\lambda}$ is a complete $\mathcal{P}_{C}$-resolution. Thus, the class of Gorenstein $C$-projective $R$-modules is closed under direct sums.

Proof  For each projective $R$-module $Q$, there is an isomorphism

$ {\rm{Hom}}_{R}(\amalg_{\Lambda}{\bf{X}}_{\lambda}, C\otimes_{R}Q)\cong \Pi_{\Lambda}{\rm{Hom}}_{R}({\bf{X}}_{\lambda}, C\otimes_{R}Q). $

So if the complex ${\rm{Hom}}_{R}({\bf{X}}_{\lambda}, C\otimes_{R}Q)$ is exact for every $\lambda$, then the complex ${\rm{Hom}}_{R}(\amalg_{\Lambda}{\bf{X}}_{\lambda}, C\otimes_{R}Q)$ is also exact. It follows that a direct sum of Gorenstein $C$-projective $R$-modules is Gorenstein $C$-projective.

Lemma 3.2 Let $0\rightarrow M'\rightarrow M\rightarrow M''\rightarrow 0$ be the exact sequence of $R$-modules and $M''$ be a Gorenstein $C$-projective $R$-module. Then $M'$ is Gorenstein $C$-projective if and only if $M$ is Gorenstein $C$-projective. Namely, the class of Gorenstein $C$-projective modules is closed under extensions and direct summands.

Proof  Firstly, assume that $M'$ and $M''$ are Gorenstein $C$-projective modules with complete $\mathcal{P}_{C}$-resolution ${\bf{X}}'$ and ${\bf{X}}''$, respectively. By Horseshoe lemma [20, Lemma 6.20] and [6, Lemma 1.13], we can construct a complex

$ {\bf{X}}: \cdots \rightarrow C\otimes_{R}P_{1} \rightarrow C\otimes_{R}P_{0} \rightarrow C\otimes_{R}P^{0} \rightarrow C\otimes_{R}P^{1} \rightarrow \cdots, $

where each $P_{i}$ and $P^{i}$ is projective, and a degreewise split exact sequence of complexes

$ {\bf{X}}: 0\rightarrow X' \rightarrow X\rightarrow X" \rightarrow 0 $

such that $M\cong$ ${\rm {Im}}$$(C\otimes_{R}P_{0}\rightarrow C\otimes_{R}P^{0})$. To show that $M$ is Gorenstein $C$-projective, it suffices to show complex ${\rm{Hom}}_{R}({\bf{X}}, C\otimes_{R}Q)$ is exact for every projective $R$-module $Q$. The sequence

$ {\bf{X}}: 0\rightarrow {\rm{Hom}}_{R}(X", C\otimes_{R}Q) \rightarrow {\rm{Hom}}_{R}(X, C\otimes_{R}Q)\rightarrow {\rm{Hom}}_{R}(X', C\otimes_{R}Q) \rightarrow 0 $

is an exact sequence of complex. Since the outer two complexes are exact, the associated long exact sequence in homology shows that the middle one is also exact.

Next, assume that $M$ and $M''$ are Gorenstein $C$-projective modules with complete $\mathcal{P}_{C}$-resolution ${\bf{X}}$ and ${\bf{X}}''$, respectively. Comparison lemma provides a morphism of chain complexes $ \varphi: {\bf{X}}\rightarrow {\bf{X}}''$ induced by $ \pi: M\rightarrow M''$ on the degree 0. By adding complexes of the form $0\rightarrow C\otimes_{R}P_{i}''\rightarrow C\otimes_{R}P_{i}''\rightarrow 0$ and $0\rightarrow C\otimes_{R}(P^{i})''\rightarrow C\otimes_{R}(P^{i})''\rightarrow 0$ to ${\bf{X}}$, we assume $\varphi$ is surjective. Since $\mathcal{P}_{C}(R)$ is closed under kernels of epimorphisms, thus the complex ${\bf{X'}}=\rm{Ker}(\varphi)$ has the form

$ {\bf{X'}}: \cdots \rightarrow C\otimes_{R}P_{1}' \rightarrow C\otimes_{R}P_{0}' \rightarrow C\otimes_{R}(P^{0})' \rightarrow C\otimes_{R}(P^{1})' \rightarrow \cdots $

with $P_{i}'$ and $(P^{i})'$ projective. The exact sequence ${\bf{X}}: 0\rightarrow X' \rightarrow X\rightarrow X" \rightarrow 0 $ is degreewise split by [6, Lemma 1.13], so an argument similar to that of the previous paragraph implies that ${\bf{X'}}$ is a complete $\mathcal{P}_{C}$-resolution and $M'$ is Gorenstein $C$-projective. Note that $\mathcal {P}_{C}(R)\subseteq\mathcal {G}\mathcal {P}_{C}(R)$, it follows from Eilenberg's Swindle [5, 1.4] that $\mathcal {G}\mathcal {P}_{C}(R)$ is closed under direct summands, as desired.

Next is a key lemma, which plays an important part in solving Question $1$ from the introduction.

Lemma 3.3  Let $M$ be an $R$-module. Then $M$ has a $\mathcal {P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact if and only if $M$ has a $\mathcal {G}\mathcal{P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact.

Proof It is enough to show the "if" part. Let $M$ has a ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact $\mathcal {G}\mathcal{P}_{C}(R)$-resolution $ \cdots \longrightarrow G_{2}\longrightarrow G_{1}\longrightarrow G_{0} \longrightarrow M \longrightarrow 0 $ with $G_{i}\in\mathcal {G}\mathcal{P}_{C}(R)$, $i\geq 0$. Set $N=\rm{Im}(G_{1}\rightarrow G_{0})$, then $0\rightarrow N\rightarrow G_{0}\rightarrow M\rightarrow 0$ be an exact sequence which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, where $G_{0} \in \mathcal {G}\mathcal {P}_{C}(R)$ and $N$ has a $\mathcal {G}\mathcal {P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Then we have the following pullback diagram

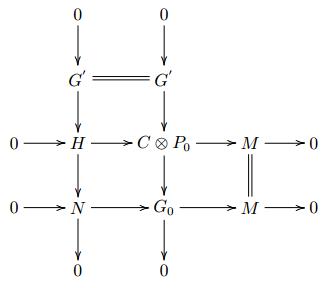with $P_{0}\in\mathcal {P}(R)$, $G' \in\mathcal{G}\mathcal {P}_{C}(R)$ and all rows and columns ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Note that there exists an exact sequence $0\rightarrow K\rightarrow G_{1}\rightarrow N\rightarrow 0, $ which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, where $G_{1} \in \mathcal {G}\mathcal {P}_{C}(R)$ and $K$ has a $\mathcal {G}\mathcal {P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Consider the following pullback diagram

The exactness of the middle row implies $L \in \mathcal {G}\mathcal {P}_{C}(R)$ by Lemma 3.2. Since the short exact sequence

$ 0\rightarrow K\rightarrow L\rightarrow H\rightarrow 0 $

is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact by Snake lemma, and $K$ has a ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact $\mathcal {G}\mathcal {P}_{C}(R)$-resolution, thus $H$ has a $\mathcal {G}\mathcal {P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Note that

$ 0\rightarrow H\rightarrow C\otimes P_{0}\rightarrow M\rightarrow 0 $

is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, $H$ and $M$ have the same properties, so by repeating the preceding process, we have that $M$ has a $\mathcal {P}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, as required.

Dually, we have the following lemma.

Lemma 3.4  Let $M$ be an $R$-module. Then $M$ has a $\mathcal {P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact if and only if $M$ has a $\mathcal {G}\mathcal{P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact.

Proof  It is enough to show the "if" part. Let $M$ has a ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact $\mathcal {G}\mathcal{P}_{C}(R)$-coresolution

$ 0 \longrightarrow M\longrightarrow G^{0}\longrightarrow G^{1} \longrightarrow G^{2}\longrightarrow \cdots $

with $G^{i}\in\mathcal {G}\mathcal{P}_{C}(R)$, $i\geq 0$. Set $N=\rm{Im}(G^{0}\rightarrow G^{1})$, then $0\rightarrow M\rightarrow G^{0}\rightarrow N\rightarrow 0 $ be an exact sequence which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, where $G^{0} \in \mathcal {G}\mathcal {P}_{C}(R)$ and $N$ has a $\mathcal {G}\mathcal {P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Then we have the following pushout diagram

with $P^{0}\in\mathcal {P}(R)$, $G_{(1)}\in\mathcal {G}\mathcal {P}_{C}(R)$ and all rows and columns ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Note that there exists an exact sequence $0\rightarrow N\rightarrow G^{1}\rightarrow K\rightarrow 0, $ which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, where $G^{1} \in \mathcal {G}\mathcal {P}_{C}(R)$ and $K$ has a $\mathcal {G}\mathcal {P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Consider the following pushout diagram.

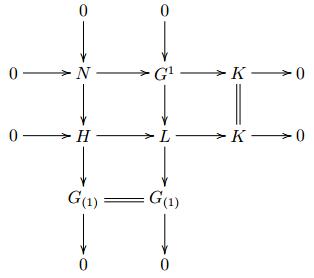The exactness of the middle column implies $L \in \mathcal {G}\mathcal {P}_{C}(R)$. Since the short exact sequence $0\rightarrow H\rightarrow L\rightarrow K\rightarrow 0$ is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact by Snake lemma, and $K$ has a ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact $\mathcal {G}\mathcal {P}_{C}(R)$-coresolution, thus $H$ has a $\mathcal {G}\mathcal{P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact. Note that $0\rightarrow M\rightarrow C\otimes P^{0}\rightarrow H\rightarrow 0$ is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact, $H$ and $M$ have the same properties, so by repeating the preceding process, we have that $M$ has a $\mathcal {P}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(-, \mathcal {P}_{C}(R))$-exact.

Let $\mathcal {G}^{2}\mathcal {P}_{C}(R)$ be the class of $R$-modules $M$ for which there exists an exact sequence of Gorenstein $C$-projective $R$-modules

$ {\bf{G}}: \cdots\rightarrow G_{1} \rightarrow G_{0} \rightarrow G^{0} \rightarrow G^{1} \rightarrow \cdots $

such that the complex ${\rm {Hom}}_{R}({\bf{G}}, {\rm C}\otimes_{R}P~)$ is exact for each $P\in \mathcal {P}(R)$ and $M\cong $ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$. It is obvious that $\mathcal {G}\mathcal {P}_{C}(R)$ $\subseteq$ $\mathcal {G}^{2}\mathcal {P}_{C}(R)$, as a consequence of Lemmas $3.3$ and $3.4$, we have the following result.

Theorem 3.5  $\mathcal {G}\mathcal {P}_{C}(R)$ = $\mathcal {G}^{2}\mathcal {P}_{C}(R)$.

Let $\mathcal {G}(\mathcal {G}\mathcal {P}_{C}(R))=\{M\in R\rm{-Mod}~| $there exists a ${\rm {Hom}}_{R}(-, H)$-exact exact sequence

$ {\bf{G}}:\cdots\rightarrow G_{1}\rightarrow G_{0}\rightarrow G^{0}\rightarrow G^{1}\rightarrow\cdots $

in $R$-Mod with all $G_{i}$ and $ G^{i}$ in $\mathcal {G}\mathcal {P}_{C}(R)$, $H\in\mathcal {G}\mathcal {P}_{C}(R)$ and $M\cong$ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$$\}$. Then $\mathcal {G}\mathcal {P}_{C}(R)$ $\subseteq$ $\mathcal{G}(\mathcal {G}\mathcal {P}_{C}(R))$ $\subseteq$ $\mathcal{G}^{2}\mathcal {P}_{C}(R)$, by Theorem 3.5, we have $\mathcal {G}\mathcal {P}_{C}(R)$ = $\mathcal {G}(\mathcal {G}\mathcal{P}_{C}(R))$ = $\mathcal {G}^{2}\mathcal {P}_{C}(R)$.

The stability of Gorenstein $C$-injective $R$-modules can be given dually.

Lemma 3.6  Let $0\rightarrow M'\rightarrow M\rightarrow M''\rightarrow 0$ be the exact sequence of $R$-modules and $M''$ be a Gorenstein $C$-injective $R$-module. Then $M'$ is Gorenstein $C$-injective if and only if $M$ is Gorenstein $C$-injective.

Lemma 3.7  Let $M$ be an $R$-module. Then $M$ has a $\mathcal {I}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(\mathcal {I}_{C}(R), -)$-exact if and only if $M$ has a $\mathcal {G}\mathcal {I}_{C}(R)$-resolution which is ${\rm {Hom}}_{R}(\mathcal {I}_{C}(R), -)$-exact.

Lemma 3.8  Let $M$ be an $R$-module. Then $M$ has a $\mathcal {I}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(\mathcal {I}_{C}(R), -)$-exact if and only if $M$ has a $\mathcal {G}\mathcal {I}_{C}(R)$-coresolution which is ${\rm {Hom}}_{R}(\mathcal {I}_{C}(R), -)$-exact.

Let $\mathcal {G}^{2}\mathcal {I}_{C}(R)$ be the class of $R$-modules $M$ for which there exists an exact sequence of Gorenstein $C$-injective $R$-modules

$ {\bf{G}}: \cdots \rightarrow G_{1} \rightarrow G_{0} \rightarrow G^{0} \rightarrow G^{1} \rightarrow \cdots $

such that the complex ${\rm {Hom}}_{R}({\rm {Hom}}_{R}(C, E), {\bf{G}})$ is exact for each $E\in \mathcal {I}(R)$ and $M\cong $ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$. It is obvious that $\mathcal {G}\mathcal {I}_{C}(R)$ $\subseteq$ $\mathcal {G}^{2}\mathcal {I}_{C}(R)$, as a consequence of Lemmas $3.7$ and $3.8$, we have the following result.

Theorem 3.9  $\mathcal {G}\mathcal {I}_{C}(R)$ = $\mathcal {G}^{2}\mathcal {I}_{C}(R)$.

Let $\mathcal {G}(\mathcal {G}\mathcal {I}_{C}(R))=\{M\in R\rm{-Mod}~| $there exists a ${\rm {Hom}}_{R}(H, -)$-exact exact sequence

$ {\bf{G}}:\cdots\rightarrow G_{1}\rightarrow G_{0}\rightarrow G^{0}\rightarrow G^{1}\rightarrow\cdots $

in $R$-Mod with all $G_{i}$ and $ G^{i}$ in $\mathcal {G}\mathcal {I}_{C}(R)$, $H\in\mathcal {G}\mathcal {I}_{C}(R)$ and $M\cong$ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$$\}$. Then $\mathcal {G}\mathcal {I}_{C}(R)$ $\subseteq$ $\mathcal{G}(\mathcal {G}\mathcal {I}_{C}(R))$ $\subseteq$ $\mathcal{G}^{2}\mathcal {I}_{C}(R)$, by Theorem 3.9, we have $\mathcal {G}\mathcal {I}_{C}(R)$ = $\mathcal {G}(\mathcal {G}\mathcal{I}_{C}(R))$ = $\mathcal {G}^{2}\mathcal {I}_{C}(R)$.

Theorem 3.5 and Theorem 3.9 give an affirmative answer to Question 1.

Finally, we discuss the stability of Gorenstein $C$-flat modules.

Lemma 3.10  Let $M$ be an $R$-module. If $\mathcal {G}\mathcal {F}_{C}(R)$ is closed under extensions, then $M$ has an $\mathcal {F}_{C}(R)$-resolution which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact if and only if $M$ has a $\mathcal {G}\mathcal {F}_{C}(R)$-resolution which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact.

Proof  It is enough to show the ``if" part. Let $0\rightarrow N\rightarrow G_{0}\rightarrow M\rightarrow 0$ be an $\mathcal {I}_{C}(R)\otimes_{R}$-exact exact sequence with $G_{0} \in \mathcal {G}\mathcal {F}_{C}(R)$ and $N$ having a $\mathcal {G}\mathcal {F}_{C}(R)$-resolution, which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact. Then we have the following pullback diagram

with $F_{0}\in \mathcal {F}(R)$, $G'\in \mathcal {G}\mathcal {F}_{C}(R)$. Since the bottom row is $\mathcal {I}_{C}(R)\otimes_{R}$-exact, so is the middle row. Note that there is an $\mathcal {I}_{C}(R)\otimes_{R}$-exact exact sequence $0\rightarrow K\rightarrow G_{1}\rightarrow N\rightarrow 0 $ with $G_{1} \in \mathcal {G}\mathcal {F}_{C}(R)$ and $K$ having a $\mathcal {G}\mathcal {F}_{C}(R)$-resolution, which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact. Consider the following pullback diagram.

Since $\mathcal {G}\mathcal {F}_{C}(R)$ is closed under extensions, $L\in \mathcal {G} \mathcal {F}_{C}(R)$. Thus, $H$ has a $\mathcal {G}\mathcal {F}_{C}(R)$-resolution, which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact. Note that $0\rightarrow H\rightarrow C\otimes F_{0}\rightarrow M\rightarrow 0$ is $\mathcal {I}_{C}(R)\otimes_{R}$-exact. By repeating the the preceding process, we have that $M$ has an $\mathcal {F}_{C}(R)$-resolution which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact.

Dually, we can prove the following lemma.

Lemma 3.11  Let $M$ be an $R$-module. If $\mathcal {G}\mathcal {F}_{C}(R)$ is closed under extensions, then $M$ has an $\mathcal {F}_{C}(R)$-coresolution which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact if and only if $M$ has a $\mathcal {G}\mathcal {F}_{C}(R)$-coresolution which is $\mathcal {I}_{C}(R)\otimes_{R}$-exact.

Let $\mathcal {G}^{2}\mathcal {F}_{C}(R)$ be the class of $R$-modules $M$ for which there exists an exact sequence of Gorenstein $C$-flat $R$-modules

$ {\bf{G}}: \cdots \rightarrow G_{1} \rightarrow G_{0} \rightarrow G^{0} \rightarrow G^{1} \rightarrow \cdots $

such that the complex ${\rm {Hom}}_{R}(C, E)\otimes_{R}{\bf{G}}$ is exact for each $E\in \mathcal {I}(R)$ and $M\cong $ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})$. It is obvious that $\mathcal {G}\mathcal {F}_{C}(R)$ $\subseteq$ $\mathcal {G}^{2}\mathcal {F}_{C}(R)$, as a consequence of Lemmas $3.10$ and $3.11$, we have the following result.

Theorem 3.12  If $\mathcal {G}\mathcal {F}_{C}(R)$ is closed under extensions, then $\mathcal {G}\mathcal {F}_{C}(R)$ = $\mathcal {G}^{2}\mathcal {F}_{C}(R)$.

Let $\mathcal {G}(\mathcal {G}\mathcal {F}_{C}(R))=\{M\in R\rm{-Mod}~| $there exists a $H\otimes_{R}$-exact exact sequence

$ {\bf{G}}:\cdots\rightarrow G_{1}\rightarrow G_{0}\rightarrow G^{0}\rightarrow G^{1}\rightarrow\cdots $

in $R$-Mod with all $G_{i}$ and $ G^{i}$ in $\mathcal {G}\mathcal {F}_{C}(R), $ $H\in\mathcal {G}\mathcal {I}_{C}(R)$ and $M\cong$ ${\rm {Im}}$$(G_{0}\rightarrow G^{0})\}$. It is obvious that $\mathcal {G}\mathcal {F}_{C}(R)$ $\subseteq$ $\mathcal{G}(\mathcal {G}\mathcal {F}_{C}(R))$ $\subseteq$ $\mathcal{G}^{2}\mathcal {F}_{C}(R)$, by Theorem 3.12, we have

$ \mathcal {G}\mathcal {F}_{C}(R)=\mathcal {G}(\mathcal {G}\mathcal{F}_{C}(R))=\mathcal {G}^{2}\mathcal {F}_{C}(R). $

Theorem 3.12 gives a partial positive answer to Question 2.