A REGULARIZED NEWTON METHOD FOR EQUALITY CONSTRAINED NONCONVEX OPTIMIZATION
1 Introduction
We consider the nonlinear equality constrained optimization problem:
| $
\begin{eqnarray}
\begin{array}{ll}
\min&f(x), \\
{\rm s.t.}&c(x)=0, \\
\end{array}
\end{eqnarray}
$ |
(1.1) |
with continuously differentiable functions: $f:R^n\rightarrow R$, and $c:R^n\rightarrow R^m$ $(m\leq n)$. Our interest is in methods for nonconvex minimization problems that ensure global convergence to first-order optimal points. These methods can be used in contemporary interior-point methods for general nonlinear optimization.
Recently, there are some progress in convergence analysis of regularized Newton methods for solving unconstrained programming problems, see [1-3]. Li et al.[1] presented two regularized Newton methods for convex minimization problems in which the Hessian of objective function at solutions may be singular. However, the convexity or at least the local convexity at a local minimizer of the problems cannot be relaxed in their algorithm. Shen et al. [4] and Ueda and Yamashita [5] extended the methods to unconstrained nonconvex minimization problems without the nonsingularity at solutions. The extended regularized Newton methods use the Armijo's size rule, and it does not contain unknown constants, e.g., the Lipschitz constant of $\nabla f$ as Polyak's method. However, as we use the method proposed in [5], the discrepancy between the reformed matrix and the Hessian increases more significantly if the norm of the gradient gets larger. This discrepancy leads the computation efficiency to decrease.
Our purposes here are to improve these methods and to generalize them from without constrained to with equality constrained optimization problem. Such a method is characterized by its use of the perturbation of the Lagrangian function's Hessian to deal with the negative curvature. The regularized Newton step is determined by solving a linear system. The method uses the linear model of a merit function to attain a sufficient reduction in a local approximation of the merit function.
Here, it should be mentioned that quasi-Newton method and Modified Newton method for equality constrained optimization. For quasi-Newton method, some assumptions are some-what restrictive. For example, the condition that the quasi-Newton approximation of the Lagrangian is uniformly bounded below by a positive constant rules out the case that the Hessians become ill conditioned, see Theorem 5.6.4 and Theorem 12.1.2 in [6]. However, in our algorithm, global convergence result is established without the uniformly positive definite of the Hessians. As to Modified Newton method, the numerical results show that our method is more robust than Modified Newton method (see Section 4).
To simplify the notation, we denote the gradient of the objective function $f$ by $g$ and write $A$ for the Jacobian of $c$ respectively, i.e., $g(x)=\nabla f(x)\in R ^n, A^T (x)=\nabla c(x)\in R^{n\times m}$. Subscripts $k$ refer to iterations indices and $f_k$ is taken to mean $f(x_k)$, $c_k$ to $c(x_k)$, $g_k$ to $g(x_k)$ and $A_k$ to $A(x_k)$, etc. For a matrix $A\in R^{n\times n}$, $\lambda_{\min}(A)$ denotes the minimum eigenvalue of $A$. Throughout the paper, $\|\cdot\|$ indicates the Euclidean vector norm.
The paper is organized as follows. In the next section the overall algorithm is developed in detail. The convergence analysis of our algorithm is finished in Section 3. In Section 4, we present some numerical results.
2 Development of the Algorithm
By introducing the Lagrangian function $L$ one can derive first-order optimality conditions. The Lagrangian function corresponding to problem (1.1) is $L(x, \lambda):= f(x)+\lambda^T c(x), $ where $\lambda\in R^m$ are the Lagrange multipliers. If $f$ and $c$ are continuously differentiable, then the first-order optimality conditions for $x^*$ to be an optimal solution to problem (1.1) state that there exist multipliers $\lambda^*$ such that $(x^*, \lambda^*)$ is a solution to the nonlinear system of equations:
| $
\begin{equation}
\ \nabla L(x, \lambda)=\left[
\begin{array}{c}
g(x)+A^T(x)\lambda \\ c(x) \\
\end{array}
\right] =0.
\end{equation}
$ |
(2.1) |
Suppose that $(x_k, \lambda_k)$ are estimate of the critical values $(x^*, \lambda^*)$. Then the Newton equations for suitable corrections $(d_k, \delta_k)$ to these estimates are simply
| $
\begin{eqnarray}
\left[
\begin{array}{cc}
H_k&A_k^T\\ A_k& 0\\
\end{array}
\right] \left[
\begin{array}{c}
d_k \\ \delta_k \\
\end{array}
\right] =- \left[
\begin{array}{c}
g_k+A_k^T\lambda_k\\c_k \end{array} \right],
\end{eqnarray}
$ |
(2.2) |
where
| $\begin{eqnarray*}
H_k:=\nabla_{xx}^2 L_k=\nabla_{xx}^2 f(x_k)+\sum\limits_{i=1}^m
\lambda_k ^i \nabla_{xx}^2 c_i(x_k)\end{eqnarray*}
$ |
is the Hessian of the Lagrangian and $\lambda_k^i$ represents the $i$th component of $\lambda_k$. If the constraint Jacobian $A_k$ has full row rank and $H_k$ is positive definite over the null space of $A_k$, then a solution to (2.2) is well defined in this context.
We are interested in the general case, i.e., $H_k$ is not always positive definite over the null space of $A_k$. Now, we generalize the technic proposed in [4, 5] for unconstrained optimization to the equality constrained case. In the equation (2.2), let $H_k$ be modified by
| $
\begin{equation}
\ W_k=H_k+[\Lambda_k+\min(\beta, \|g_k+A_k^T\lambda_k\|+\|c_k\|)]I,
\end{equation}
$ |
(2.3) |
where $\Lambda_k:=\max\{0, -\lambda_{\min}(H_k)\}$ and $\beta>0$ is a fixed constant.
Obviously, $W_k$ is positive definite when $\|g_k+A_k^T\lambda_k\|+\|c_k\|\neq 0$.
Next, we define the merit function to be $\Phi(x, \mu):=f(x)+\mu\|c(x)\|, $ where $\mu$ is a penalty parameter. We denote $\Phi{'}(d, \mu)$ as the directional derivative of the merit function $\Phi(x, \mu)$ at $x$ along $d$, and
| $
m_k(d, \mu):=f_k+g_k^T d+\mu \|c_k+A_k d\|,
$ |
as the local approximation of $\Phi(x, \mu)$ about $x_k$. The reduction in the model $m_k$ produced by $d_k$ is denoted by
| $
\begin{eqnarray*}
\Delta m_k(d_k, \mu)&:=&m_k(0, \mu)- m_k(d_k, \mu)\\
&=&-g_k^Td_k+\mu(\|c_k\|-\|c_k+A_k d_k\|)\\
&=&-g_k^Td_k+\mu\|c_k\|.
\end{eqnarray*}
$ |
After computing a step $d_k$, we require that the reduction in the model $m_k$ satisfies
| $
\begin{equation}
\Delta m_k(d_k, \mu_k)\geq \frac{1}{2}d_k^T W_k
d_k+\sigma\mu_k\|c_k\|
\end{equation}
$ |
(2.4) |
for some parameter $0 < \sigma < 1$ and appropriate $\mu_k$.
A complete statement of the algorithm is given as follows.
Algorithm A:
Let $0 < \sigma, \eta, \theta, r < 1$ and $\beta>0$ be given constants. Initialize $x_0\in R^n, \lambda_0\in R^m$, and $ \mu_0>0$. Set $k=0$.
Step 1 Evaluate functions at $x_k$.
Compute $c_k, A_k, f_k, g_k$.
Step 2 Check for termination.
If $\|g_k+A_k^T\lambda_k\|+\|c_k\|=0$, stop.
Step 3 Compute search direction.
Compute $W_k$ by using (2.3), and solve the following linear system
| $
\begin{eqnarray}
\left[
\begin{array}{cc}
W_k&A_k^T\\ A_k&0\\
\end{array}
\right] \left[
\begin{array}{c}
d \\ \delta \\
\end{array}
\right] =- \left[
\begin{array}{c}
g_k+A_k^T\lambda_k\\c_k \end{array} \right].
\end{eqnarray}
$ |
(2.5) |
Let $(d_k, \delta_k)$ be the solution of (2.5).
Step 4 Update penalty parameter $\mu_k$.
If the reduction condition (2.4) is satisfied, then go to Step 5. Otherwise, update the penalty parameter by setting
| $
\begin{eqnarray}
\mu_k=\frac{1}{(1-\sigma)\|c_k\|}(g_k^T d_k+\frac{1}{2}d_k^T W_k d_k)+\theta.
\end{eqnarray}
$ |
(2.6) |
Step 5 Backtracking line search.
Compute $\alpha_k$ with the first number $\alpha$ in sequence $\{1, r, r^2, \cdots\}$ satisfying the Armijo condition:
| $
\begin{eqnarray}
\Phi(x_k+\alpha d_k, \mu_k)\leq \Phi(x_k, \mu_k)+\alpha\eta\Phi{'}(d_k, \mu_k).
\end{eqnarray}
$ |
(2.7) |
Step 6 Update.
Set $(x_{k+1}, \lambda_{k+1})=(x_k, \lambda_k)+\alpha_k(d_k, \delta_k), \mu_{k+1}=\mu_k, k=k+1$, go back to Step 1.
3 Global Convergence
Let us begin our investigation of the well-posedness and global behavior of Algorithm A by making the following assumptions about the problem and the set of computed iterates.
Assumption 3.1 The sequence $\{x_k\}$ generated by Algorithm A is contained in a convex set $\mathcal{A}$.
Assumption 3.2 The function $f$ and $c$ and their first and second derivatives are bounded on $\mathcal{A}$.
Assumption 3.3 The sequences $\{\lambda_k\}$ and $\{W_k\}$ are bounded.
Assumption 3.4 The constraint Jacobians $A_k$ have full row rank and their small singular values are bounded below by a positive constant.
Remark 3.1 The positive definiteness of $W_k$ along with Assumption 3.4 ensures that the equation (2.5) is solvable and has unique solution.
We start by showing that Algorithm A is well defined.
Lemma 3.1 If the penalty parameter $\mu_k$ is chosen as Step 4 of Algorithm A, the inequality (2.4) is always hold.
Proof If $c_k=0$, the first block equation in (2.5) and positive definition of $W_k$ imply
| $
\begin{eqnarray*}
\Delta m_k(d_k, \mu_k)&=& -g_k^T d_k
= d_k^T W_k d_k+d_k^T A_k^T (\lambda_k+\delta_k)\\
&=& d_k^T W_k d_k-c_k^T (\lambda_k+\delta_k)
= d_k^T W_k d_k
\geq \frac{1}{2}d_k^T W_k d_k.
\end{eqnarray*}
$ |
In this case, (2.4) is satisfied for the current penalty parameter $\mu_k$.
If $c_k\neq0$ and (2.4) is not hold for the current penalty parameter $\mu_k$, then (2.6) implies the updated penalty parameter $\mu_k$ satisfies
| $
\mu_k\geq\frac{1}{(1-\sigma)\|c_k\|}(g_k^Td_k+\frac{1}{2} d_k^T W_k d_k),
$ |
i.e.,
| $
-g_k^T d_k+\mu_k\|c_k\|\geq\frac{1}{2}d_k^T W_k d_k+\sigma\mu_k\|c_k\|.
$ |
It means that (2.4) is also hold for the updated penalty parameter $\mu_k$.
Lemma 3.2 The directional derivative of the merit function $\Phi(x, \mu)$ along a step $d$ satisfies $\Phi{'}(d, \mu)=g^Td-\mu\|c\|.$
Proof We can obtain from Taylor expansion that
| $
\begin{eqnarray*}
\Phi(x+\alpha d, \mu)-\Phi(x, \mu)&=& f(x+\alpha d)-f(x)+\mu(\|c(x+\alpha d)\|-\|c(x)\|\\
&\leq& \alpha g^Td+K_1 \mu\alpha^2\|d\|^2+\mu(\|c(x)+\alpha Ad\|-\|c(x)\|)\\
&=& \alpha g^Td+K_1 \mu\alpha^2\|d\|^2+\mu(\|(1-\alpha)c(x)\|-\|c(x)\|)\\
&=& \alpha (g^Td-\mu\|c(x)\|)+K_1 \mu\alpha^2\|d\|^2,
\end{eqnarray*}
$ |
where $K_1$ is some constant. By arguing similarly, we also obtain the following lower bound:
| $
\Phi(x+\alpha d, \mu)-\Phi(x, \mu)\geq \alpha (g^Td-\mu\|c(x)\|)-K_1 \mu\alpha^2\|d\|^2.
$ |
Dividing both sides by $\alpha$ and taking the limit as $\alpha\rightarrow0$ yields the result.
A corollary to above two lemmas is that the step $d_k$ computed in Step 3 is a direction of nonincrease for the merit function $\Phi(x, \mu)$. This result allows us to show that the Armijo condition (2.7) is satisfied by some positive $\alpha_k$ (see Lemma 3.5), and so Algorithm A is well defined.
We now investigate the global property of Algorithm A. We consider the decomposition
where $u_k$, the tangential component, lies in the null apace of $A_k$ and $v_k$, the normal component, lies in the range space of $A_k^T$.
The following result shows that the normal step sequence $\{v_k\}$ is bounded.
Lemma 3.3 There exists a constant $K_2>0$ independent of the iterates such that
| $
\|v_k\|\leq K_2 \|c_k\|.
$ |
Proof From $A_k v_k=-c_k$ and the fact $v_k$ lies in the range space of $A_k^T$, it follows that
| $
v_k = A_k^T(A_kA_k^T)^{-1}A_kv_k
= A_k^T(A_kA_k^T)^{-1}(-c_k),
$ |
and so $ \|v_k\|\leq\|A_k^T(A_kA_k^T)^{-1}\|\cdot\|c_k\|.$
The fact that Assumption 3.2 and 3.4 imply that $\|c_k\|$ and $\|A_k^T(A_kA_k^T)^{-1}\|$ are bounded. Therefore there exists a constant $K_2>0$ independent of the iterates such that
| $
\|A_k^T(A_kA_k^T)^{-1}\|\leq K_2,
$ |
which implies $\|v_k\|\leq K_2 \|c_k\|$.
The next lemma shows that the penalty parameter $\mu_k$ remains bounded.
Lemma 3.4 The sequence of penalty parameters $\{\mu_k\}$ is bounded above and there exists an integer $K\geq0$ such that $\mu_k=\mu_K$ for all $k\geq K$.
Proof The penalty parameter is increased during iteration $k$ of Algorithm A only when (2.6) is invoked. From Lemma 3.1, we know that $\mu_k$ is chosen to satisfy the inequality (2.4), namely
| $
\Delta m_k(d_k, \mu_k)- \frac{1}{2}d_k^T W_k d_k\geq\sigma\mu_k\|c_k\|.
$ |
From the equation (2.5), we have
| $
W_kd_k+A_k^T\delta_k=-(g_k+A_k^T\lambda_k).
$ |
Left multiplicating both side by $u_k^T$ and using $A_ku_k=0$ yields $-g_k^Tu_k=u_k^TW_kd_k$. This, along with the equation (2.5), implies for some constant $K_3>0$ independent of the iterates,
| $
\begin{eqnarray*}
-g_k^T d_k-\frac{1}{2}d_k^T W_k d_k&=& -g_k^Tv_k-\frac{1}{2}v_k^T W_k v_k-u_k^T W_k v_k-g_k^T u_k-\frac{1}{2}u_k^T W_k u_k\\
&=& -g_k^Tv_k-\frac{1}{2}v_k^T W_k v_k+\frac{1}{2}u_k^T W_k u_k\\
&\geq& -g_k^Tv_k-\frac{1}{2}v_k^T W_k v_k
\geq -K_3\|c_k\|,
\end{eqnarray*}
$ |
the last inequality follows from Assumptions 3.2 and 3.3 and Lemma 3.3. Then, we have shown
| $
\Delta m_k(d_k, \mu_k)- \frac{1}{2}d_k^T W_k d_k\geq(\mu_k-K_3)\|c_k\|
$ |
and so (2.4) is always satisfied for $\mu_k\geq\frac{K_3}{(1-\sigma)}.$ Therefore, if $\mu_K\geq\frac{K_3}{(1-\sigma)}$ for some $K\geq 0$, then $\mu_k=\mu_K$ for all $k\geq K$. The result follows from the above and the fact that when Algorithm A increases penalty parameter it does so by at least constant $\theta>0$.
Next, we show that the line search in Step 5 will be successful.
Lemma 3.5 Suppose that there exists a constant $\varepsilon>0$ such that
| $
\|g_k+A_k^T\lambda_k\|+\|c_k\|\geq\varepsilon.
$ |
Then, for some constant $K_4>0$ independent of $\varepsilon$, $\alpha_k\geq\alpha_{\min}(\varepsilon), $ where
| $
\alpha_{\min}(\varepsilon):=\frac{(1-\eta)r\min(\beta, \varepsilon)}{2K_4\mu_K}
$ |
and $\mu_K$is from Lemma 3.4.
Proof Suppose that the line search fails for some $\bar{\alpha}>0$, then
| $
\Phi(x_k+\bar{\alpha} d_k, \mu_k)- \Phi(x_k, \mu_k)>\bar{\alpha}\eta\Phi{'}(d_k, \mu_k).
$ |
A Taylor expansion of $\Phi(x, \mu)$ about $x_k$ yields for some $K_4>0$,
| $
\Phi(x_k+\bar{\alpha} d_k, \mu_k)- \Phi(x_k, \mu_k)\leq\bar{\alpha}\Phi{'}(d_k, \mu_k)+\bar{\alpha}^2 K_4\mu_k \|d_k\|^2.
$ |
so $(\eta-1)\Phi{'}(d_k, \mu_k) < \bar{\alpha} K_4\mu_K \|d_k\|^2, $ where $\mu_K$ is from Lemma 3.4. From Lemma 3.2, the inequality (2.4) and the suppose $\|g_k+A_k^T\lambda_k\|+\|c_k\|\geq\varepsilon$, we have
| $
\begin{eqnarray*}
(\eta-1)\Phi{'}(d_k, \mu_k)&=& (1-\eta)( -g_k^T d_k+\mu_k\|c_k\|)
\geq (1-\eta)\bigg( \frac{1}{2}d_k^T W_k d_k+\sigma \mu_k\|c_k\|\bigg)\\
&\geq& \frac{1}{2}(1-\eta)d_k^T W_k d_k
\geq \frac{1}{2}(1-\eta)\min(\beta, \varepsilon )\|d_k\|^2.
\end{eqnarray*}
$ |
so $\frac{1}{2} (1-\eta)\min(\beta, \varepsilon )\|d_k\|^2 < \bar{\alpha} K_4\mu_K \|d_k\|^2, $ i.e., $\bar{\alpha}>\frac{(1-\eta)\min(\beta, \varepsilon)}{2K_4\mu_K}, $ hence, $\alpha_{\min}(\varepsilon)$ satisfies the Armijo's rule (2.7).
Now, we show the global convergence property of Algorithm A. First, we present the convergence of the iterates toward the feasible region of problem (1.1).
Theorem 3.1 Under Assumptions 3.1-3.4, if Algorithm A does not terminate finitely, then $\lim\limits_{k\rightarrow\infty}\|c_k\|=0.$
Proof Assume that $c_k$ does not tend to zero, i.e., $\limsup_{k\rightarrow\infty}\|c_k\|>0$. Let
| $
\begin{eqnarray*}
\varepsilon&:=&\frac{1}{2} \limsup\limits_{k\rightarrow\infty}\|c_k\|, \\
I_\varepsilon(k)&:=&\{j\in\{0, 1, 2, \cdots\}|j\leq k, \|c_j\|\geq
\varepsilon\}.
\end{eqnarray*}
$ |
Then, we have $\lim_{k\rightarrow\infty}|I_\varepsilon(k)|=\infty$, where $|I_\varepsilon(k)|$ denotes the number of elements of $I_\varepsilon(k)$. From Lemma 3.4, along with Lemma 3.2, inequality (2.4) and definition of $W_k$ in (2.3), for $k\geq K$ we obtain
| $
\begin{eqnarray*}
\Phi(x_K, \mu_K)-\Phi(x_{k+1}, \mu_K)&=& \sum\limits_{j=K}^{k}[\Phi(x_j, \mu_K)-\Phi(x_{j+1}, \mu_K)]\\
&\geq& -\eta\alpha_{\min}(\varepsilon)\sum\limits_{j=K}^{k} \Phi{'}(x_j, \mu_K)\\
&=& \eta\alpha_{\min}(\varepsilon)\sum\limits_{j=K}^{k} (-g_j^Td_j+\mu_K\|c_j\|)\\
&\geq& \eta\alpha_{\min}(\varepsilon)\sum\limits_{j=K}^{k} \bigg(\frac{1}{2}d_j^TW_jd_j+\sigma\mu_K\|c_j\|\bigg)\\
&\geq& \eta\alpha_{\min}(\varepsilon)\sigma\mu_K\sum\limits_{j=K}^{k} \|c_j\|\\
&\geq& \eta\alpha_{\min}(\varepsilon)\sigma\mu_K\sum\limits_{j\in I_\varepsilon(k)}\varepsilon\\
&=& \eta\alpha_{\min}(\varepsilon)\sigma\mu_K\varepsilon|I_\varepsilon(k)|.
\end{eqnarray*}
$ |
This contradicts the fact that Assumption 3.2 implies $\Phi(x, \mu_K)$ is bounded below. Hence, we have $\limsup\limits_{k\rightarrow\infty}\|c_k\|=0$, i.e., $\lim\limits_{k\rightarrow\infty}\|c_k\|=0.$
Second, we present convergent property of the reduced gradient.
Theorem 3.2 Let Assumptions 3.1-3.4 hold. If Algorithm A does not terminate finitely, then
| $\begin{eqnarray*}
\liminf\limits_{k\rightarrow\infty}\|g_k+A_k^T\lambda_k\|=0.\end{eqnarray*}
$ |
Proof We show it by contradiction. Assume that this is wrong, then possibly after increasing $K$ there exists $\varepsilon>0$ with $\|g_k+A_k^T\lambda_k\|\geq\varepsilon$ for all $k\geq K$.
In the same way as Theorem 3.1, for $k\geq K$ we have
| $
\begin{eqnarray*}
\Phi(x_K, \mu_K)-\Phi(x_{k+1}, \mu_K)&\geq& \eta\alpha_{\min}(\varepsilon)\sum\limits_{j=K}^{k} \bigg(\frac{1}{2}d_j^TW_jd_j+\sigma\mu_K\|c_j\|\bigg)\\
&\geq& \frac{1}{2}\eta\alpha_{\min}(\varepsilon)\sum\limits_{j=K}^{k} d_j^TW_jd_j\\
&\geq& \frac{1}{2}\eta\alpha_{\min}(\varepsilon)\min(\beta, \varepsilon)\sum\limits_{j=K}^k \|d_k\|^2.
\end{eqnarray*}
$ |
The fact that Assumption 3.2 implies $\Phi(x, \mu_k)$ is bounded below means $\lim\limits_{k\rightarrow\infty}\|d_k\|=0$.
An expansion of the first block of the optimality conditions (2.1) yields
| $
\|g_{k+1}+A_{k+1}^T\lambda_{k+1}\|\leq\|g_k+A_k^T\lambda_k+\alpha_k(\nabla_{xx}^2L_k d_k+A_k^T\delta_k)\|+\alpha_k^2\beta_1(d_k, \delta_k),
$ |
where
| $
\beta_1(d_k, \delta_k)=O(\|d_k\|^2+\|d_k\|\cdot\|\delta_k\|).
$ |
Employing the above inequality, the first block equation in (2.5) and the triangle inequality, we obtain for $k\geq K$,
| $
\begin{eqnarray*}
\|g_{k+1}+A_{k+1}^T\lambda_{k+1}\|&\leq&\|g_k+A_k^T\lambda_k+\alpha_k(W_k d_k+A_k^T\delta_k)+\alpha_k(\nabla_{xx}^2L_k-W_k)d_k\|\\
&&+\alpha_k^2\beta_1(d_k, \delta_k)\\
&\leq&\|g_k+A_k^T\lambda_k-\alpha_k(g_k+A_k^T\lambda_k)\|\\
&&+\alpha_k\|(\nabla_{xx}^2L_k-W_k)d_k\|+\alpha_k^2\beta_1(d_k, \delta_k)\\
&\leq&(1-\alpha_{\min}(\varepsilon))\|g_k+A_k^T\lambda_k\|\\
&&+\alpha_k\beta_2(d_k, \delta_k),
\end{eqnarray*}
$ |
where
| $
\beta_2(d_k, \delta_k)=O(\|d_k\|+\|d_k\|^2+\|d_k\|\cdot\|\delta_k\|),
$ |
and the last inequality follows from Assumptions 3.2 and 3.3 and Lemma 3.5. Note that the bound $\alpha_{\min}(\varepsilon)\leq 1$ follows from the algorithm${'}$s construction.
The boundedness of $\{\alpha_k\}$, and the fact that Assumption (3.3) implies $\delta_k$ is bounded in norm imply that
| $\begin{eqnarray*}
\lim\limits_{k\rightarrow\infty}\alpha_k\beta_2(d_k, \delta_k)=0.\end{eqnarray*}
$ |
So possibly after increasing $K$ for all $k\geq K$ we have
| $
\alpha_k\beta_2(d_k, \delta_k)<\frac{1}{2}\alpha_{\min}(\varepsilon)\varepsilon
$ |
and
| $
\begin{eqnarray*}
\|g_{k+1}+A_{k+1}^T\lambda_{k+1}\|&\leq&(1-\alpha_{\min}(\varepsilon))\|g_k+A_k^T\lambda_k\|+\frac{1}{2}\alpha_{\min}(\varepsilon)\varepsilon\\
&\leq&\|g_k+A_k^T\lambda_k\|-\frac{1}{2}\alpha_{\min}(\varepsilon)\varepsilon.
\end{eqnarray*}
$ |
Therefore, $\{\|g_k+A_k^T\lambda_k\|\}$ decreases monotonically by at least a constant amount for $k\geq K$, so we eventually find $\|g_k+A_k^T\lambda_k\|<\varepsilon$ for some $k\geq K$. This contradicts $\|g_k+A_k^T\lambda_k\|\geq \varepsilon$ for all $k\geq K$. Hence, our assumption was wrong and $\liminf\limits_{k\rightarrow\infty}\|g_k+A_k^T\lambda_k\|=0$ is hold.
4 Numerical Results
In this section, we give some numerical experiments to show the success of Algorithm A. A Matlab code was written corresponding to this implementation. We also compare the performance of Algorithm A with Modified Newton method. All examples are chosen from [7]. The parameter setting and termination criteria about the implementation are described as follows.
(1) The parameter setting. The algorithm parameters were set as follows:
| $
\sigma=0.2, \quad \eta=10^{-8}, \quad \theta=10^{-4}, \quad r=0.5, \\
\beta=0.5, \quad \lambda_0=(1, 1, \cdots, 1)\in R^m, \quad\mu_0=1.
$ |
(2) Termination criteria. Algorithm A stops if
| $
\|g_k+A_k^T\lambda_k\|+\|c_k\|\leq10^{-6}.
$ |
In Algorithm A, the left most eigenvalue of $H_k$ is computed via Matlab's eig function. Then, we compute the solution to (2.5) by factorizing the coefficient matrix using the Doolittle method.
In modified Newton method, modification is made prior to the step computation, by adding multiplies of the identity matrix to $H_k$, in order to create a strictly convex subproblem during each iteration (see Appendix B in [8]). The modification of $H_k$ is as follows:
set $p_k=10^{-4};$
while $\min({\rm eig}(H_k)) < =0$,
$H_k=H_k+p_k*I$;
$p_k=10*p_k$;
end.
$W_k=H_k$.
In table 1, which presents results of the numerical experiments, we use the following notation:
表 1
(Table 1)
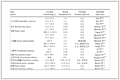
Table 1 Detailed results for test problems
| Problem |
n |
m |
Inter |
Algorithm A Final-f |
Prec |
Iter |
MN method Final-f |
Prec |
| HS6 |
2 |
1 |
17 |
1.6452e-015 |
1.0767e-007 |
10 |
1.1615e-017 |
4.7427e-009 |
| HS7 |
2 |
1 |
8 |
-1.7321 |
4.5455e-013 |
8 |
-1.7321 |
4.5455e-013 |
| HS8 |
2 |
2 |
5 |
-1 |
3.3887e-015 |
5 |
-1 |
1.9606e-015 |
| HS9 |
2 |
1 |
11 |
-0.5000 |
3.6001e-011 |
3 |
-0.5000 |
2.0854e-007 |
| HS26 |
3 |
1 |
18 |
2.1913e-012 |
7.6669e-007 |
20 |
3.4840e-011 |
8.7814e-007 |
| HS27 |
3 |
1 |
11 |
0.0400 |
9.9904e-011 |
39 |
0.0400 |
5.8248e-008 |
| HS28 |
3 |
1 |
8 |
1.5892e-022 |
1.1550e-011 |
1 |
0 |
0 |
| HS39 |
4 |
2 |
8 |
-1.0000 |
7.6740e-012 |
8 |
-1.0000 |
1.4825e-010 |
| HS40 |
4 |
3 |
11 |
-0.2500 |
7.1297e-007 |
44 |
-0.2500 |
9.7529e-007 |
| HS42 |
4 |
2 |
5 |
13.8579 |
3.3191e-011 |
4 |
13.8579 |
9.4286e-009 |
| HS46 |
5 |
2 |
20 |
1.7025e-011 |
6.6584e-007 |
20 |
1.4784e-009 |
7.7951e-007 |
| HS47 |
5 |
3 |
13 |
-1.4716e-011 |
2.7142e-007 |
|
Fail |
|
| HS48 |
5 |
2 |
5 |
9.8627e-014 |
5.4573e-007 |
2 |
8.0178e-017 |
2.0555e-008 |
| HS49 |
5 |
2 |
21 |
3.7996e-010 |
3.2629e-007 |
17 |
3.2131e-009 |
6.2142e-007 |
| HS50 |
5 |
3 |
11 |
3.1323e-021 |
1.0125e-010 |
9 |
7.2661e-019 |
3.2518e-009 |
| HS51 |
5 |
3 |
5 |
2.4961e-016 |
3.0791e-008 |
1 |
1.4791e-031 |
1.4594e-015 |
| HS52 |
5 |
3 |
5 |
5.3266 |
6.4326e-013 |
1 |
5.3266 |
4.2328e-015 |
| HS56 |
7 |
4 |
139 |
-3.4560 |
8.5290e-007 |
|
Fail |
|
| HS61 |
3 |
2 |
7 |
-143.6461 |
4.1959e-009 |
7 |
-143.6461 |
1.4535e-012 |
| HS77 |
5 |
2 |
12 |
0.2415 |
2.5399e-007 |
13 |
0.2415 |
1.3893e-007 |
| HS78 |
5 |
3 |
33 |
-2.9197 |
8.6101e-007 |
53 |
-2.9197 |
9.9956e-007 |
| HS79 |
5 |
3 |
7 |
0.0788 |
1.0003e-008 |
5 |
0.0788 |
3.4568e-007 |
|
Table 1
Detailed results for test problems
|
$n$: the number of variables,
$m$: the number of constraints,
$MN$ method: Modified Newton method,
Iter: the number of outer iterations,
Final- $f$: the final value of the objective function,
Prec: the final value of $\|g_k+A_k^T\lambda_k\|+\|c_k\|$ used in the termination criteria,
Fail: the algorithm does not terminate properly.
All the equality constrained problems proposed in [7], a total of 22, were selected. For the problem 61, because the full row rank condition described in Assumption 3.4 does not hold at the starting point, we select another point $x_0=(0, 0, 1)^T$ as the initial point. For each problem that be successfully solved by both of the methods, the number of outer iteration of these methods are similar. But, there are 2 problems where Algorithm A solved while modified Newton method could not solve. For problems 47 and 56, using modified Newton method, the outer iteration limit of 1000 can be reached before an iterate satisfies the termination criteria. Table 1 shows that Algorithm A is clearly superior to modified Newton method. The numerical results illustrate that our regularized Newton method for equality constrained nonconvex optimization is effective and more robust than modified Newton method.
5 Conclusions
A new regularized Newton method is proposed for solving equality constrained nonconvex optimizations. This method is characterized by its use of the perturbation of the Lagrangian function's Hessian to deal with the negative curvature. The global convergence properties are proved nuder reasonable assumptions. Numerical experiments are conducted to compare this method with the classical modified Newton method and results show that new method is competitive. Our approach can be extended to generally constrained problems as our methodology is applied to the equality constrained barrier subproblems arising in an interior point method.
 2015, Vol. 35
2015, Vol. 35  Issue (1): 1-11
Issue (1): 1-11 2015, Vol. 35
2015, Vol. 35  Issue (1): 1-11
Issue (1): 1-11